
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Сопряженные дифференциальные уравнения | Сопряженные дифференциальные уравнения (далее С) понятие теории дифференциальных уравнений. Уравнением, сопряженным с дифференциальным уравнением
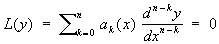 , (1) , (1)
называется уравнение
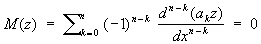 , (2) , (2)
Соотношение сопряженности взаимно. Для С имеет место тождество
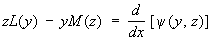 , ,
где y (у, z) — билинейная форма относительно у, z и их производных до (n - 1)-го порядка включительно. Знание k интегралов сопряженного уравнения позволяет понизить на k единиц порядок данного уравнения. Если
y1, у2,... уn (3)
— фундаментальная система решений уравнения (1), то фундаментальная система решений уравнения (2) дается формулами
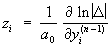 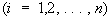 , ,
где D — определитель Вроньского (см. Вронскиан) системы (3). Если для уравнения (1) заданы краевые условия, то существуют сопряженные с ними краевые условия для уравнения (2) такие, что уравнения (1) и (2) с соответствующими краевыми условиями определяют сопряженные дифференциальные операторы (см. Сопряженные операторы). Понятие сопряженности обобщается также на системы дифференциальных уравнений и на уравнения с частными производными.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 11:34:02
|

|

|
 |
|

|
 |
 |
 |
|