
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Метрический тензор | Метрический тензор (далее М) совокупность величин, определяющих геометрические свойства пространства (его метрику). В общем случае риманова пространства n измерений метрика определяется заданием квадрата расстояния ds2 между двумя бесконечно близкими точками (x1, x2,..., xn) и (x1 + dx1, x2 + dx2,..., xn + dxn):
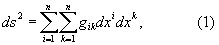
где x1, x2,..., xn — координаты, gik — некоторые функции координат. Совокупность величин gik образует тензор второго ранга, который и называется М Этот тензор симметричен, т. е. gik = gki. Вид компонент М gik зависит от выбора системы координат, однако ds2 не меняется при переходе от одной координатной системы к другой, т. е. является инвариантом относительно преобразований координат. Если выбором системы координат можно привести М к виду
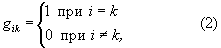
то пространство является плоским, евклидовым пространством (для трехмерного пространства ds2 = dx2 + dy2 +dz2, где x1 = х, x2 = у, x3 = z — декартовы прямоугольные координаты). Если никаким преобразованием координат нельзя привести М к виду (2), пространство является искривленным и кривизна пространства определяется М
В теории относительности М определяет метрику пространства-времени.
Лит. см. при статьях Римановы геометрии, Относительности теория, Тяготение.
Г. А. Зисман.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 12:02:26
|

|

|
 |
|

|
 |
 |
 |
|