
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Матрица (в математике) | Матрица (далее М) в математике, система элементов aij (чисел, функций или иных величин, над которыми можно производить алгебраические операции), расположенных в виде прямоугольной схемы. Если схема имеет m строк и n столбцов, то говорят о (m ´ n)-матрице. Обозначения:
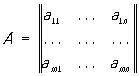 или или 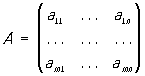 . .
Короче: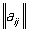 , , 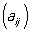 . Наряду с конечными М (в математике) рассматриваются М (в математике) с бесконечным числом строк или столбцов. . Наряду с конечными М (в математике) рассматриваются М (в математике) с бесконечным числом строк или столбцов.
М (в математике), состоящая из одной строки, называется строкой, из одного столбца - столбцом. Если m = n, то М (в математике) называется квадратной, а число n - ее порядком. Квадратная М (в математике), у которой отличны от нуля лишь диагональные элементы ai = aii называется диагональной и обозначается diag(a1, ..., an). Если все ai = a, получают скалярную М (в математике) При a = 1 М (в математике) называется единичной и обозначается Е. М (в математике), все элементы которой равны нулю, называется нулевой.
Переставив в М (в математике) строки со столбцами, получают транспонированную М (в математике) A`, или AT. Если элементы М (в математике) заменяют на комплексно-сопряженные, получают комплексно-сопряженную М (в математике) А. Если элементы транспонированной М (в математике) A` заменяют на комплексно-сопряженные, то получают М (в математике) А*, называется сопряженной с А. Определитель квадратной М (в математике) А обозначается ½A½ или det A. Минором k-го порядка М (в математике) А называется определитель k-го порядка, составленный из элементов, находящихся на пересечении некоторых k строк и k столбцов М (в математике) A в их естественном расположении. Рангом М (в математике) А называется максимальный порядок отличных от нуля миноров матрицы.
Действия над матрицами. Произведением прямоугольной (m ´ n)-матрицы А на число ее называют М (в математике), элементы которой получены из элементов aij умножением на число a:
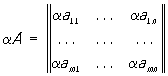
Сумма определяется для прямоугольных М (в математике) одинакового строения, и элементы суммы равны суммам соответствующих слагаемых, то есть
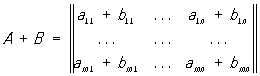
Умножение М (в математике) определяется только для прямоугольных М (в математике) таких, что число столбцов первого множителя равно числу строк второго. Произведением (m ´ р)-матрицы А на (р ´ n)-матрицу В будет (m ´ n)-матрица С с элементами
cij = ai1b1j + ai2b2j + ... + aipbpj,
i = 1, ..., m, j = 1, ..., n.
Введенные три действия над М (в математике) обладают свойствами, близкими к свойствам действий над числами. Исключением является отсутствие коммутативного закона при умножении М (в математике): равенство AB = BA может не выполняться. Матрицы А и В называются перестановочными, если AB = BA. Кроме того, произведение двух М (в математике) может равняться нулевой М (в математике), хотя каждый сомножитель отличен от нулевой. Справедливы правила:
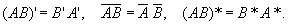
Определитель произведения двух квадратных М (в математике) равен произведению определителей перемножаемых М (в математике)
Часто удобно разбивать М (в математике) на клетки, являющиеся М (в математике) меньших размеров, проводя разделительные линии через всю М (в математике) слева направо или сверху вниз. При умножении такой так называемой клеточной М (в математике) на число, нужно умножить все ее клетки на то же число. При надлежащем согласовании разбиений действия сложения и умножения клеточных М (в математике) осуществляются так, как будто вместо клеток стоят числа.
Квадратная М (в математике) А = (aij) называется неособенной, или невырожденной, если ее определитель не равен нулю; в противном случае М (в математике) называется особенной (вырожденной). М (в математике) А-1 называется обратной к квадратной М (в математике) А, если AA-1 = E, при этом 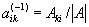 . Неособенность М (в математике) А есть необходимое и достаточное условие существования обратной М (в математике), которая при этом оказывается единственной и перестановочной с исходной М (в математике) Верна формула: (AB)-1 = -1A-1. . Неособенность М (в математике) А есть необходимое и достаточное условие существования обратной М (в математике), которая при этом оказывается единственной и перестановочной с исходной М (в математике) Верна формула: (AB)-1 = -1A-1.
Большой интерес приобретает обобщенная обратная (или псевдообратная) М (в математике) А+, определяемая как для любой прямоугольной М (в математике), так и для особенной квадратной. Эта М (в математике) определяется из четырех равенств:
AA+A = A, А+АА+ = А, AA+ = (AA+*(, А+А = (А+А*(.
Квадратные матрицы. Степенью An М (в математике) А называется произведение n сомножителей, равных А. Выражение вида a0Аn + a1An-1 + ... + anE, где a0, a1, ..., an - числа, называется значением полинома a0tn + aitn-1 + ... + anE от квадратной М (в математике) А. Правила действий над полиномами от данной М (в математике) А ничем не отличаются от правил действий над алгебраическими многочленами. Можно рассматривать и аналитические функции от М (в математике) В частности, если
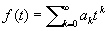
есть сходящийся на всей комплексной плоскости ряд (например, 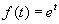 ), то и бесконечный ряд ), то и бесконечный ряд 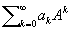 оказывается сходящимся при любой М (в математике) А, его сумму естественно считать равной f(A). Если же ряд f(t) сходится в некотором конечном круге сходимости, то f(A) задается этим рядом для достаточно "малых" М (в математике) оказывается сходящимся при любой М (в математике) А, его сумму естественно считать равной f(A). Если же ряд f(t) сходится в некотором конечном круге сходимости, то f(A) задается этим рядом для достаточно "малых" М (в математике)
Аналитические функции от М (в математике) играют большую роль в теории дифференциальных уравнений. Так, система обыкновенных дифференциальных уравнений с постоянными коэффициентами, записанных в матричных обозначениях в виде
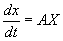
(здесь Х - столбец из неизвестных функций), имеет решение х = e, где С - столбец из произвольных постоянных.
Ненулевой столбец Х такой, что AX = lХ, называется собственным вектором М (в математике) А. В этом равенстве коэффициент l может быть лишь одним из корней многочлена
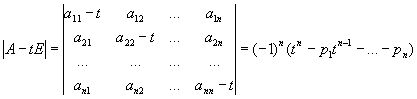
который называется характеристическим многочленом М (в математике) А. Эти корни называются собственными значениями, или характеристическими числами, М (в математике) А. Коэффициенты характеристического многочлена выражаются через суммы некоторых миноров М (в математике) А. В частности, p1 = a11 + ... + a1n = SpA (след A), 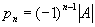 . Справедливо соотношение Кэли - Гамильтона: если j(f) есть характеристический многочлен М (в математике) А, то j(A) = 0, так что М (в математике) А является "корнем" своего характеристического многочлена. . Справедливо соотношение Кэли - Гамильтона: если j(f) есть характеристический многочлен М (в математике) А, то j(A) = 0, так что М (в математике) А является "корнем" своего характеристического многочлена.
М (в математике) А называется подобной М (в математике) В, если существует такая неособенная М (в математике) С, что В = С-1AС. Легко проверяется, что подобные М (в математике) имеют одинаковые характеристические многочлены.
Исчисление матриц. М (в математике) - полезный аппарат для исследования многих задач теоретической и прикладной математики. Одной из важнейших задач является задача нахождения решения систем линейных алгебраических уравнений. В матричных обозначениях такие системы записываются в виде
AX = ,
где A есть М (в математике) коэффициентов, Х - искомое решение, записанное в виде столбца из n элементов, - столбец свободных членов из m элементов. Если А - квадратная неособенная М (в математике), то система имеет единственное решение Х = A -1. Если A прямоугольная (m ´ n-матрица ранга k, то решение может не существовать или быть не единственным. В случае несуществования решения имеет смысл обобщенное решение, дающее минимум сумме квадратов невязок (см. Наименьших квадратов метод). При отсутствии единственности точного или обобщенного решения часто выбирают нормальное решение, то есть решение с наименьшей суммой квадратов компонент. Нормальное обобщенное решение находится по формуле Х = A + . Наиболее важен случай переопределенной системы: k = n < m. В этом случае обобщенное решение единственно. При k = m < n (недоопределенная система) точных решений бесконечно много и формула дает нормальное решение.
Не менее важной для многочисленных приложений (в теории дифференциальных уравнений, в теории малых колебаний, в квантовой механике и т. д.) является задача решения полной или частичной проблемы собственных значений. Здесь ищутся все или часть собственных значений М (в математике) и принадлежащие им собственные или корневые (некоторые обобщения собственных) векторы. К этой задаче близко примыкает и обобщенная проблема собственных значений, в которой ищутся числа и векторы такие, что AX = lBX (А и В - заданные М (в математике)), и многие родственные проблемы.
С полной проблемой непосредственно связана также задача о приведении преобразованиями подобия квадратной М (в математике) к каноническjй форме. Такой формой будет diag (l1, ..., ln), если М (в математике) имеет n различных собственных значений l1, ..., ln, или форма Жордана (см. Нормальная (жорданова) форма матрицы) в общем случае.
Ввиду большой практической важности поставленных задач для их численного решения имеется большое число различных методов. Наряду с нахождением численного решения важно оценивать качество найденного решения и исследовать устойчивость решаемой задачи.
Матрицы специального типа. Существует большое число различных типов М (в математике) в зависимости от выполнения различных соотношений между элементами.
Название матрицы
|
Определяющее условие
|
Симметричная
|
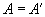
|
Кососимметричная
|
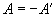
|
Ортогональная
|
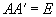 или или 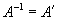
|
Стохастическая
|
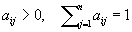
|
Эрмитова
|
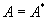
|
Унитарная
|
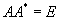 или или 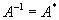
|
Некоторые типы естественно возникают в приложениях. Приведенная таблица дает ряд важных типов квадратных М (в математике)
Следует отметить также ленточные М (в математике) - такие М (в математике), ненулевые элементы которых могут располагаться на главной диагонали и на диагоналях, соседних с главной, например, двухдиагональные и трехдиагональные М (в математике) Не менее важны специальные типы М (в математике), употребляемых в качестве вспомогательных. Это элементарные М (в математике) - М (в математике), отличающиеся от единичной одним элементом; М (в математике) вращения и отражения.
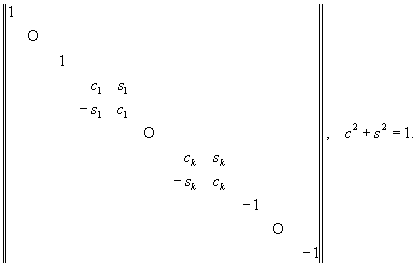
Имеются унитарные аналоги М (в математике) вращения и отражения; правые (левые) треугольные М (в математике) - М (в математике), у которых равны нулю элементы под (над) главной диагональю; правые (левые) почти треугольные М (в математике) (М (в математике) типа Хессенберга) - М (в математике), у которых равны нулю элементы под (над) диагональю, соседней снизу (сверху) с главной.
Преобразование матриц. Численные методы решения систем линейных уравнений основываются обычно на преобразовании систем посредством цепочки левых умножений на подходящие вспомогательные М (в математике) с тем, чтобы перейти к легко решаемой системе. В качестве вспомогательных для вещественных М (в математике) употребляются элементарные М (в математике), М (в математике) вращения или М (в математике) отражения. Система с неособенной М (в математике) приводится либо к системе с треугольной М (в математике), либо с ортогональной. В теоретическом аспекте это равносильно представлению М (в математике) коэффициентов в виде произведения двух треугольных М (в математике) (при выполнении некоторых дополнительных условий) или в виде произведения треугольной на ортогональную (в том или другом порядке).
Для переопределенной системы умножением слева на цепочку М (в математике) вращения или отражения можно прийти к системе с треугольной М (в математике) порядка n, решение которой дает обобщенное решение исходной системы.
Для решения проблемы собственных значений, раньше чем применять наиболее эффективные итерационные методы, целесообразно подобно преобразовать М (в математике) общего вида к М (в математике) типа Хессенберга или к трех диагональной в случае симметрии. Этого можно добиться за счет цепочки подобных преобразований элементарными М (в математике), М (в математике) вращения или М (в математике) отражения.
Историческая справка. Понятие М (в математике) было введено в работах У. Гамильтона и А. Кэли в середине 19 века. Основы теории созданы К. Вейерштрассом и Ф. Фробениусом (2-я половина 19 века и начало 20 века). И. А. Лаппо-Данилевский разработал теорию аналитических функций от многих матричных аргументов и применил эту теорию к исследованию систем дифференциальных уравнений с аналитическими коэффициентами. Матричные обозначения получили распространение в современной математике и ее приложениях. Исчисление М (в математике) развивается в направлении построения эффективных алгоритмов для численного решения основных задач.
Лит.: Смирнов В. И., Курс высшей математики, 9 изд., т. 3, ч. 1, М (в математике), 1967; Мальцев А. И., Основы линейной алгебры, 3 изд., М (в математике), 1970; Гантмахер Ф. Р., Теория матриц, 3 изд., М (в математике), 1967; Уилкинсон Дж. Х., Алгебраическая проблема собственных значений, перевод с английского, М (в математике), 1970; Фаддеев Д. К., Фаддеева В. Н., Вычислительные методы линейной алгебры, 2 изд., М (в математике) - Л., 1963; Воеводин В. В., Численные методы алгебры. Теория и алгорифмы, М (в математике), 1966; Лаппо-Данилевский И. А., Применение функций от матриц к теории линейных систем обыкновенных дифференциальных уравнений, М (в математике), 1957; Фрезер Р. А., Дункан В., Коллар А., Теория матриц и ее приложения к дифференциальным уравнениям и динамике, перевод с английского, М (в математике), 1950; Вазов В., Форсайт Дж., Разностные методы решения дифференциальных уравнений в частных производных, перевод с английского, М (в математике), 1963.
В. Н. Фаддеева. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|