
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Штурма-Лиувилля задача | Штурма - Лиувилля задача (далее Ш)задача о нахождении отличных от нуля решений дифференциального уравнения
-(p (x) y")" + q (x) y = ly, (1)
удовлетворяющих граничным условиям вида
A1y (a) + 1y"(a) = 0, А2у (b) + 2y"(b) = 0
(т. н. собственных функций), а также о нахождении значений параметра l (собственных значений), при которых существуют такие решения. При некоторых условиях на коэффициенты р (х), q (x) Ш.-Л. з. можно свести к рассмотрению аналогичной задачи для уравнения вида
-y" + q (x) y = ly. (2)
Была впервые (1837-41) исследована Ж. Лиувиллем и Ж. Ш. Ф. Штурмом.
Решение некоторых видов уравнений математической физики методом Фурье приводит к Ш.- Л. з. Например, задача о колебаниях однородной струны, закрепленной на концах, приводит к Ш.- Л. з. для уравнения -у" = lу с граничными условиями y (0) = y (p) = 0. В этом случае существует бесконечная последовательность значений 12, 22,..., n2,..., которым соответствуют собственные функции sinnx, образующие на отрезке (0, p) полную ортогональную систему функций (см. Ортогональная система функций). Аналогично обстоит дело и в общем случае, возникающем, например, при изучении распространения тепла в неоднородном стержне и т.д. И здесь, если функция q (x) в уравнении (2) непрерывна и действительна на отрезке (a, b), a A1, 1, A2, 2 - действительные числа, существует возрастающая последовательность действительных собственных значений l1,..., lп,..., стремящаяся к бесконечности, причем каждому из lп соответствует определенная с точностью до постоянного множителя собственная функция jп (х), имеющая n нулей на участке а < х < b. Функции jп (х) образуют на (а, b) полную ортогональную систему функций (для уравнения (1) имеет место ортогональность с весом р (х)). Полнота такой системы функций была доказана В. А. Стекловым в 1896. Весьма общие теоремы о разложении функций в ряды Фурье по системе jп (х) доказал Д. Гильберт (1904) с помощью теории линейных интегральных уравнений. При возрастании п собственные значения и собственные функции Ш.¾ Л. з. для уравнения (2) стремятся к собственным значениям и собственным функциям для уравнения -у" = lу при тех же граничных условиях. Большинство встречающихся в математике ортогональных систем функций, например, многочлены Лежандра, многочлены Эрмита, являются системами собственных функций некоторых Ш.- Л. з.
Иногда Ш.- Л. з. называют краевую задачу для уравнения (1) при более общих краевых условиях:
aiy (а) + biy"(а) + giy (b) + diy"(b) = 0, i = 1, 2,
где ai, bi, gi, di - постоянные числа. Среди краевых условий такого вида наиболее важными являются у (а) = у (b), y"(a)=y"(b) (периодические условия) и у (а)= -у (b), у"(а) = -y"(b) (полупериодические условия).
Многие задачи математической физики (например, задача о распространении тепла в бесконечном неоднородном стержне) приводит к Ш.- Л. з. на полуоси или на всей оси. В 1-м случае рассматриваются решения уравнения (2), удовлетворяющие условию A1y (0)+1y"(0) = 0; вместо последовательности собственных функций здесь появляется совокупность собственных функций j(х, l), зависящих от непрерывно изменяющегося параметра l. Вместо разложения в ряды Фурье рассматриваются разложения вида
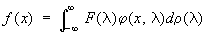 , ,
где r(l) - некоторая неубывающая функция. Эти разложения аналогичны Фурье интегралу. При этом
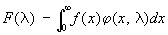
и
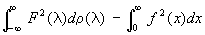 . .
Аналогичные факты имеют место и для Ш.- Л. з. на всей оси. Для некоторых задач математической физики важное значение имеет обратная Ш.-Л. з., т. е. задача о восстановлении дифференциального уравнения по функции r(l). Эта задача была поставлена в частном случае В. А. Амбарцумяном, а в более общем случае швед. математиком Г. Бортом и решена М. Г. Крейном, И. М. Гельфандом и Б. М. Левитаном.
Ш.- Л. з. возникает также в некоторых вопросах квантовой механики и вариационного исчисления.
Лит.: Курант Р., Гильберт Д., Методы математической физики, пер. с нем., 3 изд., т. 1, М.- Л., 1951; Сансоне Дж., Обыкновенные дифференциальные уравнения, пер. с итал., т. 1, М., 1953; Левитан Б. М., Разложение по собственным функциям дифференциальных уравнений второго порядка, М.- Л., 1950.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 11:52:23
|

|

|
 |
|

|
 |
 |
 |
|