
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Целая функция | Целая функция (далее Ц) функция, аналитическая во всей плоскости комплексного переменного (см. Аналитические функции). Примерами Ц могут служить алгебраический многочлен a0 + a1z +... + anzn, функции sinz, cosz, ez. Бесконечно удаленная точка является, вообще говоря, изолированной особой точкой Ц Для того чтобы бесконечно удаленная точка была устранимой особой точкой (соответственно полюсом), для Ц f (z) необходимо и достаточно, чтобы f (z) была постоянна (соответственно была алгебраическим многочленом). Если точка z = ¥ является существенно особой точкой для Ц f (z), то f (z) называют трансцендентной Ц Таковы, например, функции sinz, cosz, ez.
Для того чтобы f (z) была Ц, необходимо и достаточно, чтобы по крайней мере для одной точки z0 имело место соотношение
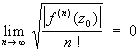
В этом случае разложение f (z) в ряд Тейлора
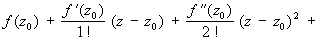
будет сходиться по всей плоскости комплексного переменного.
Основой для классификации трансцендентных Ц служит скорость роста М (r) функции, определяемой равенством
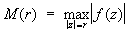
Величину
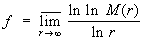
называют порядком Ц f (z). В трудах А. Пуанкаре, Ж. Адамара и Э. Бореля была установлена связь между порядком Ц и распределением ее нулей.
Лит.: Маркушевич А. И., Целые функции, М., 1965.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 25.11.2024 13:17:34
|

|

|
 |
|

|
 |
 |
 |
|