
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Характеристика (в математике) | Характеристика в (далее Х) математике, 1) целая часть десятичного логарифма.
2) Понятие теории дифференциальных уравнений с частными производными.
Характеристика (в математике) дифференциального уравнения 1-го порядка
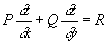 , (1) , (1)
где Р = (x, y, z), Q = Q (x, y, z), R = R (x, y, z) — заданные функции, называются кривые, определяемые системой обыкновенных дифференциальных уравнений
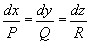 . (2) . (2)
Интегрируя систему (2), получают семейство характеристик j(x, y, z) = 1, y(x, y, z) = 2 (1, 2 — произвольные постоянные) как совокупность кривых, касающихся в каждой своей точке вектора {, Q, R}. Всякая интегральная поверхность уравнения (1) представляет собой геометрическое место Характеристика (в математике), пересекающих некоторую кривую; уравнение такой поверхности может быть записано в виде (j(x, y, z), y(x, y, z)) = 0, где — некоторая функция двух переменных. Обратно, чтобы найти интегральную поверхность, проходящую через заданную кривую (см. Коши задача), достаточно построить геометрическое место Характеристика (в математике), пересекающих эту кривую. Задача Коши имеет одно и только одно решение, если заданная кривая не является Характеристика (в математике) Понятие Характеристика (в математике) обобщается на случай дифференциального уравнения 1-го порядка с числом независимых переменных, большим двух.
Характеристика (в математике) дифференциального уравнения 2-го порядка
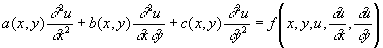 (3) (3)
были введены Г. Монжем (1784, 1795) как линии, вдоль которых удовлетворяется обыкновенное дифференциальное уравнение
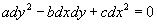 . (4) . (4)
Если уравнение (3) принадлежит к гиперболическому типу, то получаются два семейства Характеристика (в математике) с уравнениями x(x, y) = 1 и h(х, у) = 2 (1, 2 — произвольные постоянные); взяв x и h за новые аргументы, можно привести уравнение (3) к виду
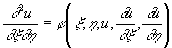 . .
Для уравнения (3) параболического типа эти семейства совпадают; если выбрать аргумент h произвольно, то уравнение (3) приведется к виду
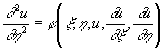 . .
Уравнение (3) эллиптического типа не имеет вещественных Характеристика (в математике); если записать решение уравнения (4) в виде x ± ih = , то уравнение (3) преобразуется к виду
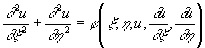 . .
Значения решения и вдоль Характеристика (в математике) и значения 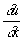 и и 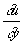 в какой-либо ее точке полностью определяют значения этих производных вдоль всей линии (на этом основан т. н. метод Характеристика (в математике) решения краевых задач для уравнения (3)); для других линий такой связи нет. С другой стороны, значения u, в какой-либо ее точке полностью определяют значения этих производных вдоль всей линии (на этом основан т. н. метод Характеристика (в математике) решения краевых задач для уравнения (3)); для других линий такой связи нет. С другой стороны, значения u, 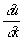 и и 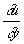 , заданные на линии, не являющейся Характеристика (в математике), определяют значения решения вблизи этой линии; для Характеристика (в математике) же это не так. Если два решения уравнения (3) совпадают по одну сторону от некоторой линии и различны по другую, то эта линия непременно является Характеристика (в математике) , заданные на линии, не являющейся Характеристика (в математике), определяют значения решения вблизи этой линии; для Характеристика (в математике) же это не так. Если два решения уравнения (3) совпадают по одну сторону от некоторой линии и различны по другую, то эта линия непременно является Характеристика (в математике)
Если коэффициенты уравнения (3) зависят от u, 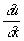 и и 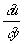 (квазилинейный случай), то Характеристика (в математике), определяемые из уравнения (4), будут разные для разных решений. Имеются определения Характеристика (в математике) и для уравнений и систем уравнений с частными производными любого порядка. (квазилинейный случай), то Характеристика (в математике), определяемые из уравнения (4), будут разные для разных решений. Имеются определения Характеристика (в математике) и для уравнений и систем уравнений с частными производными любого порядка.
Лит. см. при ст. Уравнения математической физики.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 11:46:58
|

|

|
 |
|

|
 |
 |
 |
|