Функция (математ.)

Функция (далее Ф) одно из основных понятий математики, выражающее зависимость одних переменных величин от других. Если величины x и у связаны так, что каждому значению x соответствует определенное значение у, то у называют (однозначной) функцией аргумента x. Иногда x называют независимой, а у — зависимой переменной. Записывают указанное соотношение между x и у в общем виде так: у = f (x) или у = (x) и т. п. Если связь между x и у такова, что одному и тому же значению x соответствует вообще несколько (быть может даже бесконечное множество) значений у, то у называют многозначной Ф (математ.) аргумента x. Задать Ф (математ.) у = f (x) значит указать:

1) множество А значений, которые может принимать x (область задания Ф (математ.)),

2) множество В значений, которые может принимать у (область значения Ф (математ.)), и

3) правило, по которому значениям x из А соотносятся значения у из В. В простейших случаях областью задания Ф (математ.) служит вся числовая прямая или ее отрезок а £ x £ b (или интервал а < x < b).

Правило отнесения значениям x соответствующих им значений у чаще всего задается формулой, устанавливающей, какие вычислительные операции надо произвести над x, чтобы найти у. Таковы, например, формулы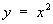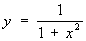

и т. п. К вычислительным (или аналитическим) операциям, кроме четырех действий арифметики, принято относить также операцию перехода к пределу (т. е. нахождение по заданной последовательности чисел a₁, a₂, a₃,... ее предела lima_n, если он существует), хотя никаких общих способов производства этой операции нет. В 1905 А. Лебег предложил общее определение аналитически изобразимой Ф (математ.) как Ф (математ.), значения которой получаются из значений x и постоянных величин при помощи арифметических действий и предельных переходов. Все т. н. элементарные Ф (математ.) sinx, cosx, a^x,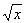

, logx, arctgx и т. п. аналитически изобразимы. Например, cosx представляется формулой:

.

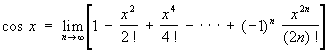В 1885 К. Вейерштрасс установил аналитическую изобразимость любой непрерывной функции. Именно, он показал, что всякая Ф (математ.), непрерывная на каком-нибудь отрезке, является пределом последовательности многочленов вида

c₀ + c₁x + c₂x² +...+ c_nxⁿ.

Кроме описанного здесь аналитического способа задания Ф (математ.) при помощи формулы, применяются и др. способы. Так, в тригонометрии Ф (математ.) cosx определяется как проекция единичного вектора на ось, образующую с ним угол в x радианов, а Ф (математ.)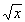

в алгебре как число, квадрат которого равен x. Возможность задания этих Ф (математ.) при помощи аналитических формул устанавливается лишь при более углубленном их изучении. Упомянем еще о т. н. функции Дирихле y(x), равной 1, если x — число рациональное, и 0, если x — число иррациональное. Впервые эта Ф (математ.) была введена этим "бесформульным" способом, но впоследствии для нее была найдена и аналитическая формула:

.

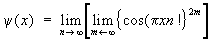Существуют, однако, и такие Ф (математ.), которые не представимы в описанном выше смысле никакой аналитической формулой. Такими Ф (математ.), во всяком случае, являются т. н. неизмеримые по Лебегу Ф (математ.)

К Ф (математ.), заданным одной аналитической формулой, примыкают Ф (математ.), которые на разных частях своей области задания определены различными формулами. Такова, например, Ф (математ.) f (x), заданная так: f (x) = x, если x £ 1, и f (x) = x², если x > 1. Приведенное выше "бесформульное" задание функции Дирихле y(x) также принадлежит к этому типу.

Ф (математ.) y = f (x) иногда задается своим графиком, т. е. множеством тех точек (x, у) плоскости, у которых x принадлежит области задания Ф (математ.), а у = f (x). В прикладных вопросах часто довольствуются таким заданием Ф (математ.), когда ее график просто начерчен на плоскости (рис.), а значения Ф (математ.) снимаются с чертежа. Так, например, верхние слои атмосферы можно изучать при помощи шаров-зондов, несущих самопишущие приборы, непосредственно доставляющие кривые изменения температуры, давления и т. п.

Чтобы задание Ф (математ.) графиком было вполне корректным с чисто математической точки зрения, недостаточно, однако, просто начертить ее график, ибо задание геометрического объекта чертежом всегда недостаточно определенно. Поэтому для графического задания Ф (математ.) должна быть указана точная геометрическая конструкция ее графика. Чаще всего эта конструкция задается при помощи уравнения, что возвращает нас к аналитическому заданию Ф (математ.), однако возможны и чисто геометрические методы построения графика (например, прямая линия вполне определяется заданием координат двух ее точек).

В технике и естествознании часто встречается следующая ситуация: зависимость между величинами x и у заведомо существует, но неизвестна. Тогда производят ряд экспериментов, в каждом из которых удается измерить одно из значений величины x и соответствующее ему значение у. В результате составляется более или менее обширная таблица, сопоставляющая измеренным значениям x соответствующие значения у. Тогда говорят о "табличном" задании Ф (математ.) Нахождение для такой Ф (математ.) аналитической формулы (см. Интерполяция) не раз представляло собой важное научное открытие (например, открытие Р. Бойлем и Э. Мариоттом формулы pv = С, связывающей давление и объем массы газа). Табличное задание Ф (математ.) с чисто математической точки зрения вполне корректно, если под областью задания Ф (математ.) понимать именно то множество значений x, которое внесено в таблицу, и табличные значения у считать абсолютно точными. Кроме Ф (математ.) одного аргумента, о которых шла речь, в математике и ее приложениях, большое значение имеют Ф (математ.) нескольких аргументов. Пусть, например, каждой системе значений трех переменных x, у, z соответствует определенное значение четвертой переменной u. Тогда говорят, что u есть (однозначная) Ф (математ.) аргументов x, у, z, и пишут u = f (x, у, z). Формулы u = x + 2y, u = (x + у) sinz дают примеры аналитического задания Ф (математ.) двух и трех аргументов. Аналогично определяются и многозначные Ф (математ.) нескольких аргументов. Ф (математ.) двух аргументов z = f (x, y) можно задать и при помощи ее графика, т. е. множества точек (x, у, z) пространства, у которых (x, у) принадлежит области задания Ф (математ.), а z = f (x, у). В простейших случаях таким графиком служит некоторая поверхность.

Развитие математики в 19 и 20 вв. привело к необходимости дальнейшего обобщения понятия Ф (математ.), заключавшегося в перенесении этого понятия с переменных действительных чисел сначала на переменные комплексные числа, а затем и на переменные математические объекты любой природы. Например, если каждому кругу x плоскости соотнести его площадь у, то у будет функцией x, хотя x уже не число, а геометрическая фигура. Точно так же, если каждому шару x трехмерного пространства соотнести его центр у, то здесь уже ни x, ни y не будут числами.

Общее определение однозначной Ф (математ.) можно сформулировать так: пусть А = {x} и В = {у} — два непустых множества, составленных из элементов любой природы, и М — множество упорядоченных пар (x, у) (где x Î А, у Î В) такое, что каждый элемент x Î А входит в одну и только одну пару из М; тогда М задает на А функцию y = f (x), значение которой для каждого отдельного x₀ Î А есть элемент y₀ Î В, входящий в единственную пару из М, имеющую x₀ своим первым элементом.

При указанном расширении понятия Ф (математ.) стирается различие между Ф (математ.) одного и нескольких аргументов. Например, всякую Ф (математ.) трех числовых переменных x, у, z можно считать Ф (математ.) одного аргумента — точки (x, у, z) трехмерного пространства. Более того, такие обобщения понятия Ф (математ.), как функционал или оператор (см. Функциональный анализ), также охватываются приведенным определением.

Как и остальные понятия математики, понятие Ф (математ.) сложилось не сразу, а прошло долгий путь развития. В работе П. Ферма "Введение и изучение плоских и телесных мест" говорится: "Всякий раз, когда в заключительном уравнении имеются две неизвестных величины, налицо имеется место". По существу здесь идет речь о функциональной зависимости и ее графическом изображении ("место" у Ферма означает линию). Изучение линий по их уравнениям в "Геометрии" Р. Декарта (1637) также указывает на ясное представление о взаимной зависимости двух переменных величин. У И. Барроу ("Лекции по геометрии", 1670) в геометрической форме устанавливается взаимная обратность действий дифференцирования и интегрирования (разумеется, без употребления самих этих терминов). Это свидетельствует уже о совершенно отчетливом владении понятием Ф (математ.) В геометрическом и механическом виде это понятие мы находим и у И. Ньютона, Однако термин "Ф (математ.)" впервые появляется лишь в 1692 у Г. Лейбница и притом не совсем в современном понимании его. Лейбниц называет Ф (математ.) различные отрезки, связанные с какой-либо кривой (например, абсциссы ее точек и т. п.). В первом печатном курсе "Анализа бесконечно малых" Г. Лопиталя (1696) термин "Ф (математ.)" не употреблялся.

Первое определение Ф (математ.) в смысле, близком к современному, встречается у И. Бернулли (1718): "Ф это величина, составленная из переменной и постоянной". В основе этого не вполне отчетливого определения лежит идея задания Ф (математ.) аналитической формулой. Та же идея выступает и в определении Л. Эйлера (см. "Введение в анализ бесконечных", 1748): "Ф переменного количества есть аналитическое выражение, составленное каким-либо образом из этого переменного количества и чисел или постоянных количеств". Впрочем, уже Эйлеру было не чуждо и современное понимание Ф (математ.), которое не связывает понятие Ф (математ.) с каким-либо аналитическим ее выражением. В его "Дифференциальном исчислении" (1755) говорится: "Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых". Все же в 18 в. отсутствовало достаточно ясное понимание различия между Ф (математ.) и ее аналитическим выражением. Это нашло отражение в той критике, которой Эйлер подверг решение задачи о колебании струны, предложенное Д. Бернулли (1753). В основе решения Бернулли лежало утверждение о возможности разложить любую Ф (математ.) в тригонометрический ряд. Возражая против этого, Эйлер указал на то, что подобная разложимость доставляла бы для любой Ф (математ.) аналитическое выражение, в то время как Ф (математ.) может и не иметь его (она может быть задана графиком, "начертанным свободным движением руки"). Эта критика убедительна и с современной точки зрения, ибо не все Ф (математ.) допускают аналитическое изображение (правда, у Бернулли речь идет о непрерывной Ф (математ.), которая всегда аналитически изобразима, но она может и не разлагаться в тригонометрический ряд). Однако другие аргументы Эйлера уже ошибочны. Например, Эйлер считал, что разложение Ф (математ.) в тригонометрический ряд доставляет для нее единое аналитическое выражение, в то время как она может быть "смешанной" Ф (математ.), представимой на разных отрезках разными формулами. На самом деле одно другому не противоречит, но в ту эпоху казалось невозможным, чтобы два аналитических выражения, совпадая на части отрезка, не совпадали на всем его протяжении.

Эти ошибочные взгляды мешали развитию теории тригонометрических рядов, и лишь в работах Ж. Фурье (1822) и П. Дирихле (1829) правильные по существу идеи Д. Бернулли получили дальнейшее развитие.

С начала 19 в. уже все чаще и чаще определяют понятие Ф (математ.) без упоминания об ее аналитическом изображении. В руководстве французского математика С. Лакруа (1810) говорится: "Всякая величина, значение которой зависит от одной или многих других величин, называется функцией этих последних". В "Аналитической теории тепла" Ж. Фурье (1822) имеется фраза: "Ф fx обозначает функцию совершенно произвольную, т. е. последовательность данных значений, подчиненных или нет общему закону и соответствующих всем значениям x, содержащимся между 0 и какой-либо величиной X". Близко к современному и определение Н. И. Лобачевского ("Об исчезании тригонометрических строк", 1834):"... Общее понятие требует, чтобы функцией от x называть число, которое дается для каждого x и вместе с x постепенно изменяется. Значение функции может быть дано или аналитическим выражением, или условием, которое подает средство испытывать все числа и выбирать одно из них, или, наконец, зависимость может существовать и оставаться неизвестной". Там же немного ниже сказано: "Обширный взгляд теории допускает существование зависимости только в том смысле, чтобы числа одни с другими в связи, понимать как бы данными вместе". Т. о., современное определение Ф (математ.), свободное от упоминаний об аналитическом задании, обычно приписываемое Дирихле и высказанное в 1837, неоднократно предлагалось и до него.

В заключение отметим следующее важное открытие, принадлежащее Д. Е. Меньшову: всякая конечная измеримая (по Лебегу) на отрезке Ф (математ.) (см. Измеримые функции) разлагается в тригонометрический ряд, сходящийся к ней почти всюду. Т. к. обычно встречаемые Ф (математ.) измеримы, то можно сказать, что практически всякая Ф (математ.) изобразима аналитически с точностью до множества меры нуль.

Лит.: Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1—2, М., 1971—73; Кудрявцев Л. Д., Математический анализ, 2 изд., т. 1—2, М., 1973; Никольский С. М., Курс математического анализа, 2 изд., т. 1—2, М.,1975

И. П. Натансон.

		Новости 21.11.2024 12:25:52

	Copyright © 1999-2024 Oval.ru, All Rights Reserved.