
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Френе формулы | Френе формулы (далее Ф) формулы, дающие разложение производных (по дуге) единичных векторов касательной t, нормали n и бинормали b произвольной кривой L по векторам t, n, b. Если k и s — кривизна и кручение L, то Ф имеют вид
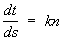 , , 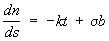 , , 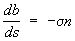 . .
С помощью Ф исследуются дифференциально-геометрические свойства кривых линий, в кинематике — движение материальной точки по криволинейной траектории.
Ф опубликованы в 1852 французским математиком Ф. Френе (. Frenet), но были известны ему еще в 1847; впервые же они были опубликованы в 1851 французским математиком Ж. Серре (J. Serret), почему их иногда называют формулами Серре — Френе.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 22.11.2024 19:47:49
|

|

|
 |
|

|
 |
 |
 |
|