
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Форма (матем.) | Форма (далее Ф) (математическая), многочлен от нескольких переменных, все члены которого имеют одну и ту же степень (под степенью одночлена хaуb... zg понимают число a + b +... + g). Теория Ф (матем.) находит применение в алгебраической геометрии, теории чисел, дифференциальной геометрии, механике и др. областях математики и ее приложений.
В зависимости от числа m переменных Ф (матем.) называют бинарными (при m = 2), тернарными (при m = 3) и т.д., в зависимости от степени n их членов – линейными (при n = 1), квадратичными (при n = 2), кубичными (при n = 3) и т.д. Например, ху + 2y2 + z2 является тернарной квадратичной Ф (матем.) Если переменные можно разбить на группы так, чтобы каждый член Ф (матем.) линейно зависел от переменных каждой группы, то Ф (матем.) называется полилинейной. Примером полилинейной Ф (матем.) является определитель, рассматриваемый как функция своих элементов (группы, на которые разбиваются в этом случае элементы, представляют собой совокупности элементов, расположенные в одинаковых строках или столбцах). Любая Ф (матем.) может быть получена из полилинейной Ф (матем.) путем отождествления некоторых переменных. Обратно – из каждой Ф (матем.) можно путем некоторого процесса, называемого процессом поляризации, получить полилинейную Ф (матем.) Например, Ф (матем.) x2 + 2x1, x2 + x2 соответствует полилинейная Ф (матем.): x1y1 + x1y2 + y1x2 + x2y2, которая в результате отождествления y1 с x1 и y2 c x2 превращается в данную Ф (матем.): x12 + 2x1x2 + x22.
Уравнение любой алгебраической кривой на плоскости может быть записано в однородных координатах в виде f (x1, x2, x3) = 0, где f – некоторая тернарная Ф (матем.) Аналогично можно дать геометрическое истолкование Ф (матем.) большего числа переменных. Геометрические свойства кривых поверхностей и т.д., не зависящие от выбора системы координат, выражаются при помощи инвариантов Ф (матем.) Теория инвариантов является одним из основных разделов алгебраической теории Ф (матем.), находящим применение не только в алгебраической геометрии, но и в ряде др. разделов математики и ее приложений.
Наиболее важными для приложений являются квадратичные формы. Например, квадрат длины вектора выражается в виде квадратичной Ф (матем.) от его координат. Если механическая система при движении остается близкой к положению равновесия, то ее кинетическая и потенциальная энергия (если они не зависят явно от времени) выражаются, соответственно, квадратичными Ф (матем.) вида:
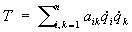 и и 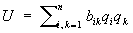 . .
Изучение колебаний таких систем основано на теории квадратичных Ф (матем.), в частности на приведении этих Ф (матем.) к сумме квадратов. Теория квадратичных Ф (матем.) тесно связана с теорией кривых и поверхностей второго порядка (см. также Эрмитова форма).
В теории чисел весьма важным является вопрос о представимости целых чисел как значений Ф (матем.) с целочисленными коэффициентами при целочисленных значениях переменных. Например, любое натуральное число представимо в виде x2 + y2 + z2 + t2 (теорема Лагранжа). Изучение вопроса о представимости целых чисел в виде ax2 + 2bxy + су2; где а, b, с, х и у – целые числа, было проведено Ж. Лагранжем и К. Гауссом. Этот вопрос тесно связан с теорией алгебраических чисел. А. Туэ доказал, что уравнения вида f (х, у) = m, где степень формы f больше двух, имеют конечное число целочисленных решений (см. Диофантовы уравнения).
В дифференциальной геометрии и римановой геометрии используются дифференциальные Ф (матем.), т. е. многочлены от дифференциалов переменных, каждый член которых имеет относительно дифференциалов одну и ту же степень. Коэффициенты дифференциальных Ф (матем.) могут произвольно зависеть от самих переменных. Рассматриваются и полилинейные дифференциальные Ф (матем.) Примерами дифференциальных Ф (матем.) являются первая и вторая квадратичные Ф (матем.) поверхностей теории. Важную роль в дифференциальной геометрии играют целые рациональные функции от коэффициентов квадратичных Ф (матем.) и их производных, не изменяющиеся при любых дифференцируемых невырождающихся преобразованиях переменных (дифференциальные инварианты). Например, полная, или гауссова, кривизна поверхности является дифференциальным инвариантом первой квадратичной Ф (матем.) Исследования по теории дифференциальных инвариантов сыграли важную роль в возникновении тензорного исчисления. Теория дифференциальных инвариантов находит большое применение в физике, позволяя давать инвариантные (не зависящие от выбора системы координат) формулировки физическим законам.
Многие теоремы интегрального исчисления (см. Грина формулы, Остроградского формула, Стокса формула) могут рассматриваться как теоремы о связи дифференциальных Ф (матем.) различной степени. Обобщая эти соотношения, Э. Картан построил теорию внешнего дифференцирования Ф (матем.), играющую важную роль в современной математике.
Лит.: Веблен О., Инварианты дифференциальных квадратичных форм, пер. с англ., М., 1948; Гуревич Г. Б., Основы теории алгебраических инвариантов, М. – Л.. 1948; Гантмахер Ф (матем.) Р., Теория матриц, 3 изд., М., 1967; Боревич З. И., Шафаревич И. Р., Теория чисел, 2 изд., М., 1972.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 11:38:43
|

|

|
 |
|

|
 |
 |
 |
|