
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Уравнение состояния | Уравнение состояния (далее У) связывает давление р, объем и температуру Т физически однородной системы в состоянии равновесия термодинамического: f (p, , Т) = 0. Это уравнение называется термическим У, в отличие от калорического У, определяющего внутреннюю энергию системы как функцию какого-либо двух из трех параметров р, , Т. Термическое У позволяет выразить давление через объем и температуру р = p (, Т) и определить элементарную работу dA = = pd при бесконечно малом расширении системы d. У является необходимым дополнением к термодинамическим законам, которое делает возможным их применение к реальным веществам. Оно не может быть выведено с помощью одних только законов термодинамики, а определяется или рассчитывается теоретически на основе представлений о строении вещества методами статистической физики. Из первого начала термодинамики следует лишь существование калорического У, а из второго начала термодинамики – связь между термическим и калорическим У 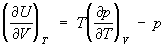 , откуда вытекает, что для идеального газа внутренняя энергия не зависит от объема , откуда вытекает, что для идеального газа внутренняя энергия не зависит от объема 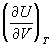 = 0. Термодинамика показывает, что для вычисления как термического, так и калорического У, достаточно знать любой из потенциалов термодинамических в виде функции своих параметров. Например, если известна Гельмгольцева энергия как функция Т и , то У находят дифференцированием: = 0. Термодинамика показывает, что для вычисления как термического, так и калорического У, достаточно знать любой из потенциалов термодинамических в виде функции своих параметров. Например, если известна Гельмгольцева энергия как функция Т и , то У находят дифференцированием:
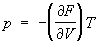 , , 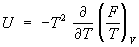 . .
Примерами У для газов может служить Клапейрона уравнение для идеального газа pu = RT, где R – газовая постоянная, u – объем 1 моля газа;
Ван-дер-Ваальса уравнение 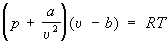 , где а и b – постоянные, зависящие от природы газа и учитывающие влияние сил притяжения между молекулами и конечность из объема, вириальное У для неидеального pu / RT = 1 + (T)/ u + С (Т)/ u2 +.., где В (Т), С (Т)... – 2-й, 3-й и т.д. вириальные коэффициенты, зависящие от сил взаимодействия между молекулами (см. Газы). Это уравнение является наиболее надежным и теоретически обоснованным У для газов и позволяет объяснить многочисленные экспериментальные результаты на основании простых моделей межмолекулярного взаимодействия. Были предложены также различные эмпирические У, основанные на экспериментальных данных о теплоемкости и сжимаемости. У неидеальных газов указывает на существование критической точки (с параметрами pk, k, Tk), в которой газообразная и жидкая фазы становятся идентичными (см. Критическое состояние). Если У представить в виде приведенного У, т. е. в безразмерных переменных p/pk, /k, T/Tk, то при не слишком низких температурах это уравнение мало меняется для различных веществ (закон соответственных состояний). , где а и b – постоянные, зависящие от природы газа и учитывающие влияние сил притяжения между молекулами и конечность из объема, вириальное У для неидеального pu / RT = 1 + (T)/ u + С (Т)/ u2 +.., где В (Т), С (Т)... – 2-й, 3-й и т.д. вириальные коэффициенты, зависящие от сил взаимодействия между молекулами (см. Газы). Это уравнение является наиболее надежным и теоретически обоснованным У для газов и позволяет объяснить многочисленные экспериментальные результаты на основании простых моделей межмолекулярного взаимодействия. Были предложены также различные эмпирические У, основанные на экспериментальных данных о теплоемкости и сжимаемости. У неидеальных газов указывает на существование критической точки (с параметрами pk, k, Tk), в которой газообразная и жидкая фазы становятся идентичными (см. Критическое состояние). Если У представить в виде приведенного У, т. е. в безразмерных переменных p/pk, /k, T/Tk, то при не слишком низких температурах это уравнение мало меняется для различных веществ (закон соответственных состояний).
Для равновесного излучения, или фотонного газа, У определяется Планка законом излучения для средней плотности энергии.
Для жидкостей из-за сложности учета всех особенностей взаимодействия молекул пока не удалось теоретически получить общее У Уравнение Ван-дер-Ваальса хотя и применяют для качественной оценки поведения жидкостей, но оно по существу неприменимо ниже критической точки, когда возможно сосуществование жидкой и газообразной фаз. У, хорошо описывающее свойства ряда простых жидкостей, можно получить из приближенных теорий жидкого состояния типа теории свободного объема или дырочной теории (см. Жидкость). Знание распределения вероятности взаимного расположения молекул (парной корреляционной функции) принципиально позволяет вычислить У жидкости, но эта задача очень сложна и полностью еще не решена даже с помощью вычислительных машин.
Для твердых тел термическое У определяет зависимость модулей упругости от температуры и давления. Оно может быть получено на основании теории теплового движения в рассматривающей фононы и их взаимодействие, но пока общего У для твердых тел не найдено.
Для сред элементарная работа при намагничивании равна dA = -НdМ, где М – момент, Н – напряженность поля. Следовательно, зависимость М = М (Н, Т) представляет собой У
Для электрически поляризуемых сред элементарная работа при поляризации равна dA = -ЕdР где Р - поляризация, Е - напряженность электрического поля, следовательно, У имеет вид Р = (Е, Т).
Лит.: Хилл Т., Статистическая механика, пер. с англ., М., 1960; Вукалович М. П., Новиков И. И., У реальных газов, М. – Л., 1948; Мейсон Э., Сперлинг Т., Вириальное уравнение состояния, пер. с англ., М., 1972; Лейбфрид Г., Людвиг В., Теория ангармонических эффектов в пер. с англ., М., 1963. См. также лит. при статьях Статистическая физика и Термодинамика.
Д. Н. Зубарев.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 13:26:03
|

|

|
 |
|

|
 |
 |
 |
|