
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Уникурсальная кривая | Уникурсальная кривая (далее У) (от уни… и лат. cursus - бег, путь) (матем.), плоская кривая,, которая может быть задана параметрическими уравнениями x = j (t), y = y (t), где j (t) и y (t) - рациональные функции параметра t. Важнейшие теоремы об У: если алгебраическая кривая имеет максимальное число двойных точек, допускаемое ее порядком, то она уникурсальна; обратная ей: всякая У является алгебраической кривой с максимальным числом двойных точек, допускаемых ее порядком. В формулировке этих теорем предполагается, что точки высшей кратности пересчитаны по определенным правилам на двойные (например, одна тройная точка эквивалентна трем двойным).
Максимальное число двойных точек, которое может иметь алгебраическая кривая n-ого порядка, равно (n – 1)(n – 2)/2 = d. Если кривая n-ого порядка имеет r двойных точек, то разность d - r, т. е. число двойных точек, недостающее до максимального числа, называется дефектом, или родом, этой кривой. У может быть также поэтому определена как алгебраическая кривая, род которой равен нулю. Очевидно, что прямая линия и кривая 2-го порядка не могут иметь двойных точек, следовательно, они всегда уникурсальны. Кривая 3-го порядка уникурсальна, если она имеет одну двойную точку, кривая 4-го порядка уникурсальна, если она имеет три двойные точки, и т. д.
На рис. изображена кривая 3-го порядка, называемая декартовым листом; она имеет одну двойную точку и, следовательно, уникурсальна. В самом деле, она может быть задана параметрическими уравнениями:
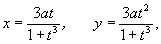
где параметр t равен тангенсу угла наклона радиус-вектора точки (x, y) к оси Ox.
При подсчете двойных точек нельзя основываться на внешнем виде кривой, т. к. двойные точки могут быть бесконечно удаленными или мнимыми. Например, кривая 4-го порядка - лемниската Бернулли, имеет одну лишь действительную двойную точку, но она имеет еще две двойные точки в мнимых круговых точках и, следовательно, уникурсальна.
У играют важную роль в теории интегралов алгебраических функций. Всякий интеграл вида
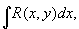
где R(x, y) есть рациональная функция двух переменных, а y есть функция от x, определяемая уравнением (x, y) = 0, задающим У, приводится к интегралу от рациональной функции и выражается в элементарных функциях.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 12:10:36
|

|

|
 |
|

|
 |
 |
 |
|