|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Существенно особая точка | Существенно особая точка (далее С)аналитической функции, точка z0 комплексной плоскости, в которой не существует ни конечного, ни бесконечного предела при z ® z0 для функции, однозначной и аналитической в некоторой окрестности этой точки (см. Аналитические функции). Примеры: точка z = 0 является Существенно особая точка для функции 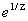 ,  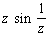,  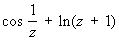и т. д. В окрестности Существенно особая точка z0 функция f (z) может быть разложена в Лорана ряд
 ,
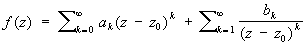причем среди чисел b1, b2,... бесконечно много отличных от нуля. Это свойство часто используется для определения Существенно особая точка О поведении функции в окрестности Существенно особая точка позволяет судить Сохоцкого-Вейерштрасса теорема. Обобщением этой теоремы служит большая теорема Пикара: во всякой окрестности Существенно особая точка аналитическая функция принимает любое комплексное значение, кроме, быть может, одного. Последняя теорема, в свою очередь, имеет ряд обобщений и уточнений. В некоторых отделах теории аналитических функций под Существенно особая точка понимают также особые точки более сложной природы.
Лит.: Маркушевич А. И., Теория. аналитических функций, 2 изд., т. 1-2, М., 1967-68; Неванлинна Р., Однозначные аналитические функции, пер. с нем., М.- Л., 1941. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 21.11.2024 12:29:26
|
|
|
|
|
|
|
|
|
|
|
