
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Стирлинга формула | Стирлинга формула (далее С) формула, дающая приближенное выражение произведения п первых натуральных чисел (т. н. факториала) 1×2×...×n = n!, когда число п сомножителей велико. С была найдена (без оценки погрешности) Дж. Стирлингом, опубликовавшим ее в 1730. С устанавливает приближенное равенство
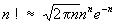 , ,
где p = 3,14159..., е = 2,71828... (основание натуральных логарифмов), причем относительная ошибка при пользовании этой формулой для вычисления n! меньше e1/12n - 1 и, таким образом, стремится к нулю при неограниченном возрастании n. Например, при n = 10 С дает n! " 3598700, тогда как точное значение 10! = 3628800; относительная ошибка в данном случае составляет менее 1%. С имеет многочисленные применения в приложениях математики, особенно в теории вероятностей и математической статистике.
Лит.: Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 2, М., 1969.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 12:01:14
|

|

|
 |
|

|
 |
 |
 |
|