
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Статистическая физика | Статистическая физика (далее С) раздел физики, задача которого — выразить свойства макроскопических тел, т. е. систем, состоящих из очень большого числа одинаковых частиц (молекул, электронов и т.д.), через свойства этих частиц и взаимодействие между ними.
Изучением макроскопических тел занимаются и др. разделы физики — термодинамика, механика сплошных сред, электродинамика сплошных сред. Однако при решении конкретных задач методами этих дисциплин в соответствующие уравнения всегда входят неизвестные параметры или функции, характеризующие данное тело. Так, для решения задач гидродинамики необходимо знать уравнение состояния жидкости или газа, т. е. зависимость плотности от температуры и давления, теплоемкость жидкости, ее коэффициент вязкости и т.п. Все эти зависимости и параметры можно, разумеется, определять экспериментально, поэтому методы, о которых идет речь, называются феноменологическими. Статистическая же физика позволяет, по крайней мере в принципе, а во многих случаях и фактически, вычислить все эти величины, если известны силы взаимодействия между молекулами. Т. о., С использует сведения о "микроскопическом" строении тел — о том, из каких частиц они состоят, как эти частицы взаимодействуют, поэтому ее называют микроскопической теорией.
Если в какой-то момент времени заданы координаты и скорости всех частиц тела и известен закон их взаимодействия, то, решая уравнения механики, можно было бы найти эти координаты и скорости в любой последующий момент времени и тем самым полностью определить состояние исследуемого тела. (Для простоты изложение ведется на языке классической механики. Но и в квантовой механике ситуация та же: зная начальную волновую функцию системы и закон взаимодействия частиц, можно, решая Шредингера уравнение, найти волновую функцию, определяющую состояние системы во все будущие моменты времени.) Фактически, однако, такой путь построения микроскопической теории невозможен, т.к. число частиц в макроскопических телах очень велико. Например, в 1 см3 газа при температуре 0 °С и давлении в 1 атм содержится примерно 2,7×1019 молекул. Невозможно решить такое число уравнений, а начальные координаты и скорости всех молекул все равно неизвестны.
Однако именно большое число частиц в макроскопических телах приводит к появлению новых — статистических — закономерностей в поведении таких тел. Это поведение в широких пределах не зависит от конкретных начальных условий — от точных значений начальных координат и скоростей частиц. Важнейшее проявление этой независимости — известный из опыта факт, что система, предоставленная самой себе, т. е. изолированная от внешних воздействий, с течением времени приходит в некоторое равновесное состояние (термодинамическое, или статистическое, равновесие), свойства которого определяются только такими общими характеристиками начального состояния, как число частиц, их суммарная энергия и т.п. (см. Равновесие термодинамическое). В дальнейшем речь будет идти главным образом о С равновесных состояний.
Прежде чем сформулировать теорию, описывающую статистические закономерности, следует разумно ограничить сами требования к теории. Именно, задачей теории должно являться вычисление не точных значений различных физических величин для макроскопических тел, а средних значений этих величин по времени. Рассмотрим, например, молекулы, находящиеся в некотором выделенном в газе достаточно большом — макроскопическом — объеме. Число таких молекул с течением времени будет меняться из-за их движения, и его можно было бы найти точно, если были бы известны все координаты молекул во все моменты времени. В этом, однако, нет необходимости. Изменение числа молекул в объеме будет носить характер беспорядочных колебаний — флуктуаций — относительно некоторого среднего значения. При большом числе частиц в объеме эти колебания будут малы по сравнению со средним числом частиц, так что для характеристики макроскопического состояния достаточно знать именно это среднее значение.
Для уяснения характера статистических закономерностей рассмотрим еще один простой пример. Пусть в некоторый сосуд помещено большое число зерен двух сортов, каждого сорта поровну, и содержимое сосуда тщательно перемешано. Тогда на основании повседневного опыта можно быть уверенным, что во взятой из сосуда пробе, содержащей все еще большое число зерен, будет обнаружено примерно равное число зерен каждого сорта независимо от того, в каком порядке засыпались зерна в сосуд. На этом примере хорошо видны два важных обстоятельства, обеспечивающих применимость статистической теории. Во первых, необходимость большого числа зерен как во всей "системе" — сосуде с зерном, так и в выбранной для опыта "подсистеме" — пробе. (Если проба состоит всего из двух зерен, то нередко оба будут одного сорта.) Во-вторых, ясно, что существенную роль играет сложность движения зерен при перемешивании, обеспечивающая их равномерное распределение в объеме сосуда.
Функция распределения. Рассмотрим систему, состоящую из частиц, для простоты считая, что частицы не имеют внутренних степеней свободы. Такая система описывается заданием 6 переменных — 3 координат qi и 3 импульсов pi, частиц (совокупность этих переменных сокращенно будет обозначаться (р, q)). Вычислим среднее значение по интервалу временит некоторой величины (р, q), являющейся функцией этих координат и импульсов. Для этого разобьем интервал (0, t) на s равных малых отрезков Dta (а = 1,2,....... s). Тогда по определению
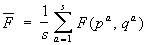 , ,
или (1)
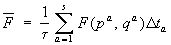 , ,
где qa и pa — значения координат и импульсов в моменты времени ta. В пределе s ® ¥ сумма переходит в интеграл:
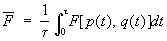 (1a) (1a)
Понятие функции распределения естественным образом, возникает, если рассмотреть пространство 6 измерений, на осях которого отложены значения координат и импульсов частиц системы; оно называется фазовым пространством. Каждому значению времени t соответствуют определенные значения всех q и р, т. е. некоторая точка в фазовом пространстве, изображающая состояние системы в данный момент времени t. Разобьем все фазовое пространство на элементы, размер которых мал по сравнению с характерными для данного состояния системы значениями q и р, но еще настолько велик, что в каждом из них находится много точек, изображающих состояние системы в различные моменты времени t. Тогда число таких точек в элементе объема будет примерно пропорционально величине этого объема dpdq. Если обозначить коэффициент пропорциональности через sw(p, q), то это число для элемента с центром в некоторой точке (р, q) запишется в виде:
da = sw (р, q) dpdq, (2)
где
dpdq = dp1dq1dp2dq2... dp3dq3
— объем выбранного элемента фазового пространства. Среднее значение (1) с учетом малости этих элементов объема можно переписать как 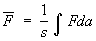 , т. е. , т. е.
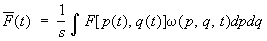 (3) (3)
(интегрирование по координатам производится по всему объему системы, по импульсам — от —¥ до ¥). Функция w(p, q, t) носит название функции распределения по координатами импульсам частиц. Поскольку полное число выбранных точек равно s, функция w удовлетворяет условию нормировки:
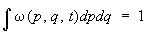 (4) (4)
Из (3) и (4) видно, что wdpdq можно рассматривать как вероятность системе находиться в элементе dpdq фазового пространства. Введенной таким образом функции распределения можно дать и др. истолкование. Для этого будем рассматривать одновременно большое число одинаковых систем и примем, что каждая точка в фазовом пространстве изображает состояние одной такой системы. Тогда усреднение по времени в (1)—(1a) можно понимать как усреднение по совокупности этих систем, или, как говорят, по статистическому ансамблю. Проведенные до сих пор рассуждения носили чисто формальный характер, т.к. нахождение функции распределения, согласно (2), требует знания всех р и q во все моменты времени, т. е. решения уравнений движения с соответствующими начальными условиями. Основным положением С является, однако, утверждение о возможности определить эту функцию из общих соображений для системы, находящейся в состоянии термодинамического равновесия. Прежде всего можно показать, исходя из сохранения числа систем при движении, что функция распределения является интегралом движения системы, т. е. остается постоянной, если р и q меняются в соответствии с уравнениями движения (см. Лиувилля теорема). При движении замкнутой системы не меняется ее энергия, поэтому все точки в фазовом пространстве, изображающие состояние системы в разные моменты времени, должны лежать на некоторой "гиперповерхности", соответствующей начальному значению энергии Е. Уравнение этой поверхности имеет вид;
(p, q) = E,
где Н (р, q) — энергия системы, выраженная через координаты и импульсы, т. е. ее функция Гамильтона. Далее, движение системы из многих частиц носит крайне запутанный характер. Поэтому с течением времени точки, описывающие состояние, распределятся по поверхности постоянной энергии равномерно, подобно тому как равномерно распределяются зерна при перемешивании в сосуде в упомянутом выше примере (см. также Эргодическая гипотеза). Такое равномерное распределение по изоэнергетической поверхности описывается функцией распределения вида:
w(p, q) = Ad( (p, q) — E), (5)
где d(Н (р, q) — E) — дельта-функция, отличная от нуля только при Н = Е, т. е. на этой поверхности, А — постоянная, определяемая из условия нормировки (4). Функция распределения (5), называется микроканонической, позволяет вычислять средние значения всех физических величин по формуле (3), не решая уравнений движения.
При выводе выражения (5) предполагалось, что единственная сохраняющаяся при движении системы величина, от которой зависит w, — это энергия системы. Разумеется, сохраняются также импульс и момент импульса, но эти величины можно исключить, предположив, что рассматриваемое тело заключено в неподвижный ящик, которому частицы могут отдавать импульс и момент.
Фактически обычно рассматриваются не замкнутые системы, а макроскопические тела, являющиеся макроскопически малыми частями, или подсистемами, какой-либо замкнутой системы. Функция распределения для подсистемы будет отлична от (5), но не будет зависеть от конкретного характера остальной части системы — т. н. термостата. Поэтому функцию распределения подсистемы можно определить, считая, например, что термостат состоит просто из частиц идеального газа, координаты и импульсы которых будем обозначать через Q и Р, в отличие от обозначений q и р для подсистемы, тогда микроканоническое распределение:
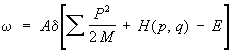
Здесь Н (р, q) — функция Гамильтона подсистемы, М — масса частицы газа, а суммирование производится по всем составляющим импульсов всех частиц термостата. Чтобы найти функцию распределения для подсистемы, нужно проинтегрировать это выражение по координатам и импульсам частиц термостата. Если затем учесть, что число частиц в термостате много больше, чем в подсистеме, и устремить ®¥, считая, что отношение E/ постоянно и равно 3/2kT, то для функции распределения подсистемы получится выражение:
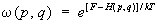 (6) (6)
Величина T в этой формуле имеет смысл температуры, k = 1,38×10-16 эрг/град — постоянная Больцмана. (Условие E/ ® 3/2kT для газа в термостате соответствует, как и должно быть, формуле (13) для идеального газа; см. ниже.) Нормировочный коэффициент e/kT определяется из условия нормировки (4):
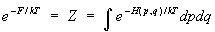 (6a) (6a)
Распределение (6) называется каноническим распределением Гиббса, или просто каноническим распределением (см. Гиббса распределение), а величина Z — статистическим интегралом. В отличие от микроканонического распределения, энергия системы в распределении Гиббса не задана. Состояния системы сосредоточены в тонком, но конечной толщины слое вокруг энергетической поверхности, соответствующей среднему значению энергии, что означает возможность обмена энергией с термостатом. В остальном в применении к определенному макроскопическому телу оба распределения приводят по существу к одним и тем же результатам. Разница лишь в том, что при использовании микроканонического распределения все средние значения оказываются выраженными через энергию тела, а при использовании канонического распределения — через температуру. Если тело состоит из двух невзаимодействующих частей 1 и 2 с функциями Гамильтона 1 и 2, то для всего тела Н = 1 + 2 и, согласно (6), функция распределения тела разбивается на произведение функций распределения для каждой из частей, так что эти части оказываются статистически независимыми. Это требование вместе с теоремой Лиувилля можно положить в основу вывода распределения Гиббса, не обращаясь к микроканоническому распределению. Формула (6) справедлива для систем, которые описываются классической механикой.
В квантовой механике энергетический спектр системы конечного объема дискретен. Вероятность подсистеме находиться в состоянии с энергией En дается формулой, аналогичной (6):
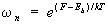 , (7) , (7)
причем условие нормировки 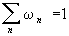 можно переписать в виде: можно переписать в виде:
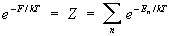 . (8) . (8)
Величина Z называется статистической суммой системы; сумма в выражении (8) берется по всем состояниям системы.
Для системы, с достаточной точностью описывающейся классической механикой, в формуле (8) можно перейти от суммирования по состояниям к интегрированию по координатам и импульсам системы, При этом на каждое квантовое состояние приходится в фазовом пространстве "клетка" (или "ячейка") объемом 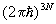 , где , где 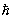 — Планка постоянная. Иными словами, суммирование по n сводится к интегрированию по — Планка постоянная. Иными словами, суммирование по n сводится к интегрированию по 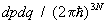 . Следует также учесть, что ввиду тождественности частиц в квантовой механике при их перестановке состояние системы не меняется. Поэтому, если интегрировать по всем р и q, необходимо поделить интеграл на число перестановок из частиц, т. е. на ! Окончательно классический предел для статистической суммы имеет вид: . Следует также учесть, что ввиду тождественности частиц в квантовой механике при их перестановке состояние системы не меняется. Поэтому, если интегрировать по всем р и q, необходимо поделить интеграл на число перестановок из частиц, т. е. на ! Окончательно классический предел для статистической суммы имеет вид:
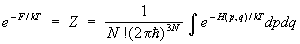 (8а) (8а)
Он отличается множителем от чисто классического условия нормировки (6а), что приводит к дополнительному слагаемому в .
Приведенные формулы относятся к случаю, когда число частиц в подсистеме задано. Если выбрать в качестве подсистемы определенный элемент объема всей системы, через поверхность которого частицы могут покидать подсистему и возвращаться в нее, то вероятность нахождения подсистемы в состоянии с энергией En и числом частиц n дается формулой большого канонического распределения Гиббса:
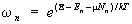 , (9) , (9)
в которой дополнительный параметр m — химический потенциал, определяющий среднее число частиц в подсистеме, а величина определяется из условия нормировки (см. формулу (11)).
Статистическое истолкование термодинамики. Важнейший результат С — установление статистического смысла термодинамических величин. Это дает возможность вывести законы термодинамики из основных представлений С и вычислять термодинамические величины для конкретных систем. Прежде всего термодинамическая внутренняя энергия отождествляется со средней энергией системы. Первое начало термодинамики получает тогда очевидное истолкование как выражение закона сохранения энергии при движении составляющих тело частиц.
Далее, пусть функция Гамильтона системы зависит от некоторого параметра l (координаты стенки сосуда, в который заключена система, внешнего поля и т.п.). Тогда производная 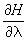 будет обобщенной силой, соответствующей этому параметру, а величина будет обобщенной силой, соответствующей этому параметру, а величина 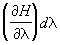 после усреднения дает механическую работу, совершаемую над системой при изменении этого параметра. Если продифференцировать выражение после усреднения дает механическую работу, совершаемую над системой при изменении этого параметра. Если продифференцировать выражение 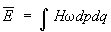 для средней энергии для средней энергии 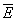 системы с учетом формулы (6) и условия нормировки, считая переменными l и T и учитывая, что величина тоже является функцией от этих переменных, то получится тождество: системы с учетом формулы (6) и условия нормировки, считая переменными l и T и учитывая, что величина тоже является функцией от этих переменных, то получится тождество:
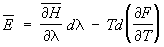 . .
Согласно сказанному выше, член, содержащий dl, равен средней работе dA, совершаемой над телом. Тогда последний член есть получаемое телом тепло. Сравнивая это выражение с соотношением dE = dA + TdS, представляющим собой объединенную запись первого и второго начал термодинамики (см. Второе начало термодинамики) для обратимых процессов, находим, что T в (6) действительно равна абсолютной температуре тела, а производная 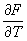 — взятой с обратным знаком энтропии . Это означает, что есть свободная энергия тела, откуда выясняется ее статистический смысл. — взятой с обратным знаком энтропии . Это означает, что есть свободная энергия тела, откуда выясняется ее статистический смысл.
Особое значение имеет статистическое истолкование энтропии, которое следует из формулы (8). Формально суммирование g этой формуле производится по всем состояниям с энергией En, но фактически ввиду малости флуктуаций энергии в распределении Гиббса существенно лишь относительно небольшое их число с энергией вблизи средней энергии. Число этих существенных состояний 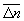 естественно определить поэтому, ограничив суммирование в (8) интервалом естественно определить поэтому, ограничив суммирование в (8) интервалом 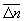 , заменив En на среднюю энергию , заменив En на среднюю энергию 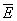 и вынося экспоненту из-под знака суммы. Тогда сумма даст и вынося экспоненту из-под знака суммы. Тогда сумма даст 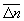 и примет вид. и примет вид.
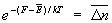
С др. стороны, согласно термодинамике, = 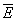 — TS, что дает связь энтропии с числом микроскопических состояний — TS, что дает связь энтропии с числом микроскопических состояний 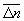 в данном макроскопическом состоянии, иначе говоря, — со статистическим весом макроскопического состояния, т. е. с его вероятностью: в данном макроскопическом состоянии, иначе говоря, — со статистическим весом макроскопического состояния, т. е. с его вероятностью:
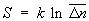 . (10) . (10)
При температуре абсолютного нуля любая система находится в определенном основном состоянии, так что 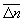 = 1, = 0. Это утверждение выражает собой третье начало термодинамики. Здесь существенно, что для однозначного определения энтропии нужно пользоваться именно квантовой формулой (8); в чисто классической статистике энтропия определена только с точностью до произвольного слагаемого. = 1, = 0. Это утверждение выражает собой третье начало термодинамики. Здесь существенно, что для однозначного определения энтропии нужно пользоваться именно квантовой формулой (8); в чисто классической статистике энтропия определена только с точностью до произвольного слагаемого.
Смысл энтропии как меры вероятности состояния сохраняется и по отношению к произвольным — не обязательно равновесным — состояниям. В состоянии равновесия энтропия имеет максимальное возможное в данных внешних условиях значение. Это означает, что равновесное состояние является состоянием с максимальным статистическим весом, наиболее вероятным состоянием. Процесс перехода системы из неравновесного состояния в равновесное есть процесс перехода из менее вероятных состояний в более вероятные; это выясняет статистический смысл закона возрастания энтропии, согласно которому энтропия замкнутой системы может только увеличиваться.
Формула (8), связывающая свободную энергию со статистической суммой, является основой для вычисления термодинамических величин методами С Она используется, в частности, для построения статистической теории электрических и свойств вещества. Например, для вычисления момента тела в поле следует вычислить статистическую сумму и свободную энергию. момент m тела дается тогда формулой:
m = 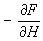 , ,
где Н — напряженность внешнего поля. Аналогично (8) условие нормировки в большом каноническом распределении (9) определяет термодинамический потенциал согласно формуле:
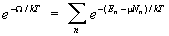 . (11) . (11)
Этот потенциал связан со свободной энергией соотношением:
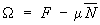 . .
Приложения С к изучению тех или иных свойств конкретных систем сводятся по существу к приближенному вычислению статистической суммы с учетом специфических свойств системы.
Во многих случаях эта задача упрощается применением закона равнораспределения по степеням свободы, утверждающего, что теплоемкость cv (при постоянном объеме v) системы взаимодействующих материальных точек — частиц, совершающих гармонические колебания, равна
cv = k (l/2 + n),
где l — общее число поступательных и вращательных степеней свободы, n — число колебательных степеней свободы. Доказательство закона основано на том, что функция Гамильтона Н такой системы имеет вид: Н = (pi) + (qm), где кинетическая энергия К — однородная квадратичная функция от l + n импульсов pi а потенциальная энергия — квадратичная функция от n колебательных координат qm. В статистическом интеграле Z (8а) интегрирование по колебательным координатам ввиду быстрой сходимости интеграла можно распространить от - ¥ до ¥. Сделав после этого замену переменных 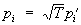 , , 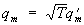 находим, что Z зависит от температуры как T l/2+n, так что свободная энергия = — kT (l/2 + n)(lnT+ const). Отсюда следует приведенное выше выражение для теплоемкости, поскольку находим, что Z зависит от температуры как T l/2+n, так что свободная энергия = — kT (l/2 + n)(lnT+ const). Отсюда следует приведенное выше выражение для теплоемкости, поскольку 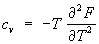 . Отклонения от закона равнораспределения в реальных системах связаны прежде всего с квантовыми поправками, т.к. в квантовой С этот закон несправедлив. Существуют также поправки, связанные с негармоничностью колебаний. . Отклонения от закона равнораспределения в реальных системах связаны прежде всего с квантовыми поправками, т.к. в квантовой С этот закон несправедлив. Существуют также поправки, связанные с негармоничностью колебаний.
Идеальный газ. Простейшим объектом исследования С является идеальный газ, т. е. газ настолько разреженный, что можно пренебречь взаимодействием между его молекулами. Термодинамические функции такого газа можно вычислить до конца. Энергия газа равна просто сумме энергий отдельных молекул. Этого, однако, еще недостаточно, чтобы считать молекулы полностью независимыми. Действительно, в квантовой механике, даже если силы взаимодействия между частицами отсутствуют, существует определенное влияние одинаковых (тождественных) частиц друг на друга, если они находятся в близких квантовомеханических состояниях. Это т. н. обменное взаимодействие. Им можно пренебречь, если на одно состояние приходится в среднем много меньше одной частицы, что во всяком случае имеет место при достаточно высокой температуре газа; такой газ называется невырожденным. Фактически обычные газы, состоящие из и молекул, невырождены при всех температурах (при которых они еще газообразны). Для невырожденного идеального газа функция распределения распадается на произведение функций распределения для отдельных молекул. лежат в интервалах dpx, dpy, dpz, а координаты — в интервалах dx, dy, dz:
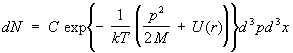 , (12) Энергия молекулы одноатомного газа во внешнем поле с потенциальной энергией (r) равна p2/2M + (r). Интегрируя (6) по координатам r (x, у, z) и импульсам р (рх, py, pz) всех молекул, кроме одной, можно найти число молекул dN, импульсы которых , (12) Энергия молекулы одноатомного газа во внешнем поле с потенциальной энергией (r) равна p2/2M + (r). Интегрируя (6) по координатам r (x, у, z) и импульсам р (рх, py, pz) всех молекул, кроме одной, можно найти число молекул dN, импульсы которых
где d3p = dpxdpydpz, d3x = dxdydz. Эта формула называется распределением Максвелла — Больцмана (см. Больцмана статистика). Если проинтегрировать (12) по импульсам, то получится формула для распределения частиц по координатам во внешнем поле, в частности в поле тяготения — барометрическая формула. Распределение же по скоростям в каждой точке пространства совпадает с Максвелла распределением.
Статистическая сумма идеального газа также распадается на произведение одинаковых членов, соответствующих отдельным молекулам. Для одноатомного газа суммирование в (8) сводится к интегрированию по координатам и импульсам, т. е. сумма заменяется на интеграл по 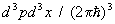 3 в соответствии с числом ячеек (с объемом 3 в соответствии с числом ячеек (с объемом 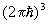 ) в фазовом пространстве одной частицы. Свободная энергия газа равна: ) в фазовом пространстве одной частицы. Свободная энергия газа равна:
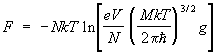 , ,
где g — статистический вес основного состояния т. е. число состояний, соответствующее его нижнему энергетическому уровню, — объем газа (здесь е — основание натуральных логарифмов). При высоких температурах g = (2J + 1)(2L + 1), где J — величина спина, a L — момента орбитального (в единицах 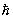 ). Из выражения для свободной энергии следует, что уравнение состояния идеального газа, т. е. зависимость его давления (Р) от плотности числа частиц (/) и температуры, имеет вид: = NkT. Внутренняя энергия одноатомного газа и его теплоемкость при постоянном объеме оказываются равными: ). Из выражения для свободной энергии следует, что уравнение состояния идеального газа, т. е. зависимость его давления (Р) от плотности числа частиц (/) и температуры, имеет вид: = NkT. Внутренняя энергия одноатомного газа и его теплоемкость при постоянном объеме оказываются равными:
Е = 3/2(NkT), v = 3/2Nk, (13)
а его потенциал:
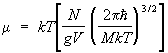 . (14) . (14)
Характерно, что даже для невырожденного (т. е. с достаточной точностью подчиняющегося классической механике) газа выражения для свободной энергии и потенциала содержат постоянную Планка 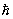 . Это, в конечном счете, обусловлено отмеченной ранее связью энтропии с понятием числа квантовых состояний. . Это, в конечном счете, обусловлено отмеченной ранее связью энтропии с понятием числа квантовых состояний.
В случае двухатомных и многоатомных газов вклад в термодинамические функции вносят также колебания и вращение молекул. Этот вклад зависит от того, существенны ли эффекты квантования колебаний и вращения молекулы. Расстояние между колебательными уровнями энергии имеет порядок 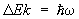 , где w — характерная частота колебаний, а расстояние между первыми вращательными уровнями энергии порядка , где w — характерная частота колебаний, а расстояние между первыми вращательными уровнями энергии порядка 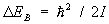 , где — момент инерции вращающегося тела, в данном случае молекулы. Классическая статистика справедлива, если температура достаточно высока, так что , где — момент инерции вращающегося тела, в данном случае молекулы. Классическая статистика справедлива, если температура достаточно высока, так что
kT >> DE.
В этом случае в соответствии с законом равнораспределения вращение вносит в теплоемкость постоянный вклад, равный 1/2k на каждую вращательную степень свободы; в частности, для двухатомных молекул этот вклад равен k. Колебания же вносят в теплоемкость вклад, равный k на каждую колебательную степень свободы (так что колебательная теплоемкость двухатомной молекулы равна k). Вдвое больший вклад колебательной степени свободы по сравнению с вращательной связан с тем, что при колебаниях в молекуле имеют не только кинетическую, но и потенциальную энергию. В обратном предельном случае 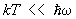 молекулы находятся в своем основном колебательном состоянии, энергия которого не зависит от температуры, так что колебания вообще не вносят вклада в теплоемкость. То же относится к вращению молекул при условии молекулы находятся в своем основном колебательном состоянии, энергия которого не зависит от температуры, так что колебания вообще не вносят вклада в теплоемкость. То же относится к вращению молекул при условии 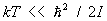 . По мере повышения температуры появляются молекулы, находящиеся в возбужденных колебательных и вращательных состояниях, и эти степени свободы начинают давать вклад в теплоемкость — как бы постепенно "включаются", стремясь при дальнейшем повышении температуры к своему классическому пределу. Т. о., учет квантовых эффектов позволил объяснить экспериментально наблюдаемую зависимость теплоемкости газов от температуры. Значения величины . По мере повышения температуры появляются молекулы, находящиеся в возбужденных колебательных и вращательных состояниях, и эти степени свободы начинают давать вклад в теплоемкость — как бы постепенно "включаются", стремясь при дальнейшем повышении температуры к своему классическому пределу. Т. о., учет квантовых эффектов позволил объяснить экспериментально наблюдаемую зависимость теплоемкости газов от температуры. Значения величины 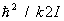 , характеризующей "вращательный квант", для большинства молекул порядка нескольких градусов или десятков градусов (85 К для 2, 2,4 К для 2, 15 К для ). В то же время характерные значения величины , характеризующей "вращательный квант", для большинства молекул порядка нескольких градусов или десятков градусов (85 К для 2, 2,4 К для 2, 15 К для ). В то же время характерные значения величины 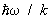 для "колебательного кванта" порядка тысяч градусов (6100 К для 2, 2700 К для 2, 4100 К для ). Поэтому вращательные степени свободы включаются при гораздо более низких температурах, чем колебательные. На рис. 1 изображены температурная зависимость вращательной (а) и колебательной (б) теплоемкостей для двухатомной молекулы (вращательная теплоемкость построена для молекулы из разных для "колебательного кванта" порядка тысяч градусов (6100 К для 2, 2700 К для 2, 4100 К для ). Поэтому вращательные степени свободы включаются при гораздо более низких температурах, чем колебательные. На рис. 1 изображены температурная зависимость вращательной (а) и колебательной (б) теплоемкостей для двухатомной молекулы (вращательная теплоемкость построена для молекулы из разных
Неидеальный газ. Важное достижение С — вычисление поправок к термодинамическим величинам газа, связанных с взаимодействием между его частицами. С этой точки зрения уравнение состояния идеального газа является первым членом разложения давления реального газа по степеням плотности числа частиц, поскольку всякий газ при достаточно малой плотности ведет себя как идеальный. С повышением плотности начинают играть роль поправки к уравнению состояния, связанные с взаимодействием. Они приводят к появлению в выражении для давления членов с более высокими степенями плотности числа частиц, так что давление изображается т. н. вириальным рядом вида:
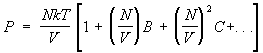 . (15) . (15)
Коэффициенты В, С и т.д. зависят от температуры и наываются. вторым, третьим и т.д. вириальными коэффициентами. Методы С позволяют вычислить эти коэффициенты, если известен закон взаимодействия между молекулами газа. При этом коэффициенты В, С,... описывают одновременное взаимодействие двух, трех и большего числа молекул. Например, если газ одноатомный и потенциальная энергия взаимодействия его (r), то второй вириальный коэффициент равен
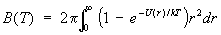 . (16) . (16)
По порядку величины В равен 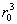 , где r0 — характерный размер или, точнее, радиус действия межатомных сил. Это означает, что ряд (15) фактически представляет собой разложение по степеням безразмерного параметра Nr3/, малого для достаточно разреженного газа. Взаимодействие между газа носит характер отталкивания на близких расстояниях и притяжения на далеких. Это приводит к тому, что В > 0 при высоких температурах и В < 0 при низких. Поэтому давление реального газа при высоких температурах больше давления идеального газа той же плотности, а при низких — меньше. Так, например, для при Т = 15,3 К коэффициент В = —3×10-23 см3, а при T = 510 К В = 1,8 ×10-23 см3. Для В = —7,1×10-23 см3 при Т = 180 К и В = 4,2×10-23 см3 при Т = 6000 К. Для одноатомных газов вычислены значения вириальных коэффициентов, включая пятый, что позволяет описывать поведение газов в достаточно широком интервале плотностей (см. также Газы). , где r0 — характерный размер или, точнее, радиус действия межатомных сил. Это означает, что ряд (15) фактически представляет собой разложение по степеням безразмерного параметра Nr3/, малого для достаточно разреженного газа. Взаимодействие между газа носит характер отталкивания на близких расстояниях и притяжения на далеких. Это приводит к тому, что В > 0 при высоких температурах и В < 0 при низких. Поэтому давление реального газа при высоких температурах больше давления идеального газа той же плотности, а при низких — меньше. Так, например, для при Т = 15,3 К коэффициент В = —3×10-23 см3, а при T = 510 К В = 1,8 ×10-23 см3. Для В = —7,1×10-23 см3 при Т = 180 К и В = 4,2×10-23 см3 при Т = 6000 К. Для одноатомных газов вычислены значения вириальных коэффициентов, включая пятый, что позволяет описывать поведение газов в достаточно широком интервале плотностей (см. также Газы).
Плазма. Особый случай неидеального газа представляет собой плазма — частично или полностью ионизованный газ, в котором поэтому имеются свободные электроны и ионы. При достаточно малой плотности свойства плазмы близки к свойствам идеального газа. При вычислении же отклонений от идеальности существенно, что электроны и ионы взаимодействуют электростатически по закону Кулона. Кулоновские силы медленно убывают с расстоянием, и это приводит к тому, что уже для вычисления первой поправки к термодинамическим функциям необходимо учитывать взаимодействие не двух, а сразу большого количества частиц, поскольку интеграл во втором вириальном коэффициенте (16), описывающий парное взаимодействие, расходится на больших расстояниях r между частицами. В действительности под влиянием кулоновских сил распределение ионов и электронов в плазме изменяется таким образом, что поле каждой частицы экранируется, т. е. быстро убывает на некотором расстоянии, называемом дебаевским радиусом. Для простейшего случая плазмы, состоящей из электронов и однозарядных ионов, дебаевский радиус rD равен:
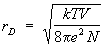 , (17) , (17)
где число электронов, е — заряд электрона. Все частицы, находящиеся внутри дебаевского радиуса, принимают участие во взаимодействии одновременно. Это приводит к тому, что первая поправка к давлению пропорциональна не (/)2 как в обычном газе, а более низкой степени плотности — (/)3/2. Количественный расчет основан на том, что остальные частицы распределены в поле выбранного электрона или иона согласно распределению Больцмана. В результате уравнение состояния с учетом первой поправки имеет вид:
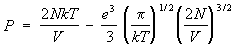 (18) (18)
(т.к. число электронов равно числу ионов, полное число частиц равно 2). Такого же рода поправки возникают и в термодинамических функциях электролитов, в которых имеются свободные ионы растворенных веществ.
Жидкости. В отличие от газа, связанные с взаимодействием члены в уравнении состояния жидкости не малы. Поэтому свойства жидкости сильно зависят от конкретного характера взаимодействия между ее молекулами. В теории жидкости вообще отсутствует малый параметр, который можно было бы использовать для упрощения теории. Невозможно получить какие-либо аналитические формулы для термодинамических величин жидкости. Одним из способов преодоления этой трудности является изучение системы, состоящей из сравнительно небольшого числа частиц — порядка нескольких тысяч. В этом случае, используя ЭВМ, можно провести прямое решение уравнений движения частиц и определить таким способом средние значения всех характеризующих систему величин без дополнительных предположений. При этом можно исследовать также и процесс приближения такой системы к состоянию равновесия. Можно также найти статистический интеграл для такой системы из небольшого числа частиц путем вычисления на ЭВМ интегралов в основной формуле для статистического интеграла (обычно при этом используется Монте-Карло метод). Полученные обоими способами результаты имеют, однако, малую точность в приложении к реальным жидкостям из-за малого числа частиц в системе.
Еще один способ построения теории жидкости основан на использовании функций распределения молекул. Если проинтегрировать функцию распределения w системы по импульсам всех частиц и по координатам всех частиц, кроме одной, получится одночастичная пространственная функция распределения f1(r). Если проинтегрировать w по импульсам всех частиц и по координатам всех частиц, кроме двух, получится двухчастичная функция распределения f2(r1, r2), всех частиц, кроме трех, — трехчастичная функция распределения f3(r1, r2, r3,) и т.д. Двухчастичная функция распределения является непосредственно наблюдаемой физической величиной — через нее выражается, например, упругое рассеяние рентгеновских лучей и нейтронов в жидкости. Считая, что функция распределения всей системы дается распределением Гиббса (6), можно получить интегральное соотношение, выражающее двухчастичную функцию через трехчастичную и потенциал взаимодействия между частицами. В теории жидкости это точное соотношение дополняется некоторыми приближенными, выражающими трехчастичную функцию через двухчастичную (одночастичная функция в однородной жидкости сводится к постоянной). В результате получается уравнение для двухчастичной функции, которое решается численно. Дополнительные соотношения находятся на основании правдоподобных физических соображений и носят интерполяционный характер, так что основанные на них теории могут претендовать лишь на качественное описание свойств жидкости. Тем не менее даже такое качественное описание имеет важное значение, поскольку в нем проявляется общность законов С (см. также Жидкость).
равновесие. Большое значение имеет предоставляемая С возможность вычисления констант равновесия, определяющих равновесные концентрации реагирующих веществ. Термодинамическая теория приводит к условию равновесия в виде равенства нулю некоторой линейной комбинации потенциалов этих веществ. В случае реакции между газами потенциалы определяются формулами, аналогичными формуле (14) для одноатомного газа, и константу равновесия можно вычислить, если известна теплота реакции. В выражения для потенциалов входит постоянная Планка, поэтому квантовые эффекты существенны даже для реакций между классическими газами. Важным частным случаем формул равновесия является Саха формула, определяющая равновесную степень ионизации газа. (Подробнее см. Равновесие химическое.)
Вырожденные газы. Если понижать температуру газа при постоянной плотности, начинают проявляться квантово-механические эффекты, связанные со свойствами симметрии волновых функций системы одинаковых частиц. Газ "вырождается" (см. Вырожденный газ). Для частиц с полуцелым спином волновая функция должна менять знак при перестановке любой пары частиц. Это, в частности, приводит к тому, что в одном квантовом состоянии не может находиться больше одной частицы (Паули принцип). Количество частиц с целым спином в одном состоянии может быть любым, но требуемая в этом случае неизменность волновой функции при перестановке частиц и здесь приводит к изменению статистических свойств газа. Частицы с полуцелым спином описываются статистикой — Дирака; их называют фермионами. К относятся, например, электроны, протоны, нейтроны, дейтерия, легкого изотопа 3Не. Частицы с целым спином — бозоны — описываются статистикой Бозе — Эйнштейна. К ним относятся 4Не, кванты света — фотоны.
Пусть среднее число частиц газа в единице объема с импульсами, лежащими в интервале d3p, есть 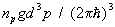 , так что np — число частиц в одной ячейке фазового пространства (g = 2J + 1, где J — спин частицы). Тогда из распределения Гиббса следует, что для идеальных газов (верхний знак) и бозонов (нижний знак): , так что np — число частиц в одной ячейке фазового пространства (g = 2J + 1, где J — спин частицы). Тогда из распределения Гиббса следует, что для идеальных газов (верхний знак) и бозонов (нижний знак):
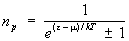 . (19) . (19)
В этой формуле e = p2/2M — энергия частицы с импульсом р, m — потенциал, определяемый из условия постоянства числа частиц () в системе:
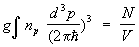 . .
Формула (19) переходит в формулу распределения Больцмана (12) при 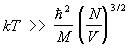 ; левая сторона этого неравенства делается порядка правой при таких температурах, при которых длина волны де Бройля частиц, движущихся с тепловой скоростью, становится порядка среднего расстояния между ними. Т. о., вырождение сказывается при температурах тем более низких, чем меньше плотность числа частиц в газе (и чем больше масса частицы М). ; левая сторона этого неравенства делается порядка правой при таких температурах, при которых длина волны де Бройля частиц, движущихся с тепловой скоростью, становится порядка среднего расстояния между ними. Т. о., вырождение сказывается при температурах тем более низких, чем меньше плотность числа частиц в газе (и чем больше масса частицы М).
В случае как и должно быть, np £ 1. Это приводит к тому, что частицы газа ( и при Т = 0 обладают отличными от нуля импульсами, поскольку в состоянии с нулевым импульсом может находиться только одна частица. Точнее, при Т = 0 для np = 1 внутри Ферми поверхности — сферы в импульсном пространстве с радиусом 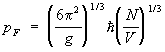 , а вне этой "ферми-сферы" np = 0. При конечных, но низких температурах np меняется от 1 внутри сферы до нуля вне сферы постепенно, причем ширина переходной области порядка MkT/p. Величина np для как функция от энергии e изображена схематически на рис. 2 (e0 = p2/2M). При изменении температуры газа меняется состояние частиц только в этом переходном слое, и теплоемкость при низких температурах пропорциональна Т и равна: , а вне этой "ферми-сферы" np = 0. При конечных, но низких температурах np меняется от 1 внутри сферы до нуля вне сферы постепенно, причем ширина переходной области порядка MkT/p. Величина np для как функция от энергии e изображена схематически на рис. 2 (e0 = p2/2M). При изменении температуры газа меняется состояние частиц только в этом переходном слое, и теплоемкость при низких температурах пропорциональна Т и равна:
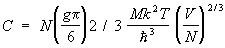 . (20) . (20)
В бозе-газе при Т = 0 все частицы находятся в состоянии с нулевым импульсом. При достаточно низких температурах в состоянии с р = 0 находится конечная доля всех частиц; эти частицы образуют т. н. бозе-эйнштейновский конденсат. Остальные частицы находятся в состояниях с р ¹ 0, причем их число определяется формулой (19) с m = 0. При температуре 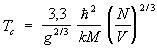 в бозе-газе происходит фазовый переход (см. ниже). Доля частиц с нулевым импульсом обращается в нуль Бозе — Эйнштейна конденсация исчезает. Кривая зависимости теплоемкости от температуры имеет в точке Tc излом. Распределение частиц по импульсам при Т > Тс дается формулой (19) причем m < 0. Схематически функции распределения Максвелла, — Дирака и Бозе — Эйнштейна (при Т > Тс) изображены на рис 3. в бозе-газе происходит фазовый переход (см. ниже). Доля частиц с нулевым импульсом обращается в нуль Бозе — Эйнштейна конденсация исчезает. Кривая зависимости теплоемкости от температуры имеет в точке Tc излом. Распределение частиц по импульсам при Т > Тс дается формулой (19) причем m < 0. Схематически функции распределения Максвелла, — Дирака и Бозе — Эйнштейна (при Т > Тс) изображены на рис 3.
Особым случаем применения статистики Бозе — Эйнштейна является равновесное электромагнитное излучение, которое можно рассматривать как газ, состоящий из фотонов. Энергия фотона связана с его импульсом соотношением 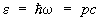 , где с — скорость света в вакууме. Число фотонов не является заданной величиной, а само определяется из условия термодинамического равновесия, поэтому их распределение по импульсам дается формулой (19) с m = 0 (причем e= рс). Распределение энергии в спектре излучения получается умножением числа фотонов на энергию e, так что плотность энергии в интервале частот dw равна , где с — скорость света в вакууме. Число фотонов не является заданной величиной, а само определяется из условия термодинамического равновесия, поэтому их распределение по импульсам дается формулой (19) с m = 0 (причем e= рс). Распределение энергии в спектре излучения получается умножением числа фотонов на энергию e, так что плотность энергии в интервале частот dw равна 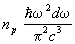 , причем np берется при , причем np берется при 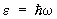 . Т. о. получается формула Планка для спектра равновесного (черного) излучения (см. Планка закон излучения). . Т. о. получается формула Планка для спектра равновесного (черного) излучения (см. Планка закон излучения).
решетка. Применение С к вычислению термодинамических функций решетки основано на том, что в решетке совершают малые колебания около своих положений равновесия. Это позволяет рассматривать решетку как совокупность связанных гармонических осцилляторов. В такой системе могут распространяться волны, характеризующиеся своим законом дисперсии, т. е. зависимостью частоты w от волнового вектора k. В квантовой механике эти волны можно рассматривать как совокупность т. н. элементарных возбуждений, или квазичастиц — фононов, обладающих энергией 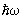 и квазиимпульсом ћk. Основное отличие квазиимпульса от импульса состоит в том, что энергия фонона является периодической функцией квазиимпульса с периодом, по порядку величины равным и квазиимпульсом ћk. Основное отличие квазиимпульса от импульса состоит в том, что энергия фонона является периодической функцией квазиимпульса с периодом, по порядку величины равным 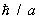 , где а — постоянная решетки. Функция распределения фононов по квазиимпульсам дается формулой распределения Бозе—Эйнштейна (19) с m = 0. При этом , где а — постоянная решетки. Функция распределения фононов по квазиимпульсам дается формулой распределения Бозе—Эйнштейна (19) с m = 0. При этом 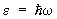 . Т. о., знание зависимости w(k) позволяет вычислить теплоемкость решетки. Эту зависимость можно определить из опытов по неупругому рассеянию нейтронов в (см. Нейтронография) или вычислить теоретически, задавая значения "силовых констант", определяющих взаимодействие в решетке. При низких температурах существенны только фононы с малой частотой, соответствующие квантам обычных звуковых волн, для которых связь w с k линейна. Это приводит к тому, что теплоемкость решетки пропорциональна T3. При высоких температурах можно пользоваться законом равного распределения энергии по степеням свободы, так что теплоемкость не зависит от температуры и равна 3Nk, где — число в . Т. о., знание зависимости w(k) позволяет вычислить теплоемкость решетки. Эту зависимость можно определить из опытов по неупругому рассеянию нейтронов в (см. Нейтронография) или вычислить теоретически, задавая значения "силовых констант", определяющих взаимодействие в решетке. При низких температурах существенны только фононы с малой частотой, соответствующие квантам обычных звуковых волн, для которых связь w с k линейна. Это приводит к тому, что теплоемкость решетки пропорциональна T3. При высоких температурах можно пользоваться законом равного распределения энергии по степеням свободы, так что теплоемкость не зависит от температуры и равна 3Nk, где — число в
Металлы. В металлах вклад в термодинамические функции дают также электроны проводимости. Состояние электрона в металле характеризуется квазиимпульсом, и, т.к. электроны подчиняются статистике — Дирака, их распределение по квазиимпульсам дается формулой (19). Поэтому теплоемкость электронного газа, а следовательно, и всего металла при достаточно низких температурах пропорциональна Т. Отличие от свободных частиц состоит в том, что поверхность около которой сосредоточены "активные" электроны, уже не является сферой, а представляет собой некоторую сложную поверхность в пространстве квазиимпульсов. Форму поверхности равно как и зависимость энергии от квазиимпульса вблизи этой поверхности, можно определять экспериментально, главным образом исследуя свойства металлов, а также рассчитывать теоретически, используя т. н. модель квазипотенциала. В сверхпроводниках (см. Сверхпроводимость) возбужденные состояния электрона отделены от щелью конечной ширины, что приводит к экспоненциальной зависимости электронной теплоемкости от температуры. В ферромагнитных и антиферромагнитных веществах вклад в термодинамические функции дают также колебания моментов — спиновые волны.
В диэлектриках и полупроводниках при Т = 0 свободные электроны отсутствуют. При конечных температурах в них появляются заряженные квазичастицы — электроны с отрицательным зарядом и (в равном числе) "дырки" с положительным зарядом, Электрон и дырка могут образовать связанное состояние — квазичастицу, называемую экситоном. Др. тип экситона представляет собой возбужденное состояние диэлектрика, перемещающееся в решетке.
Методы квантовой теории поля в С При решении задач квантовой С, прежде всего при исследовании свойств квантовых жидкостей, электронов в металлах и магнетиков, важное значение имеют методы квантовой теории поля, введенные в С сравнительно недавно. Основную роль в этих методах играет функция Грина G макроскопической системы, аналогичная функции Грина в квантовой теории поля. Она зависит от энергии e и импульса р, закон дисперсии квазичастиц e(р) определяется из уравнения:
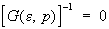 , (21) , (21)
т. е. энергия квазичастицы определяется полюсом функции Грина. Существует регулярный метод вычисления функций Грина в виде ряда по степеням энергии взаимодействия между частицами. Каждый член этого ряда содержит многократные интегралы по энергиям и импульсам от функций Грина невзаимодействующих частиц и может быть изображен графически в виде диаграмм, аналогичных Фейнмана диаграммам в квантовой электродинамике. Каждая из этих диаграмм имеет определенный физический смысл, что позволяет отделить в бесконечном ряду члены, ответственные за интересующее явление, и просуммировать их. Существует также диаграммная техника для вычисления температурных функций Грина, позволяющих вычислять термодинамические величины непосредственно, без введения квазичастиц. Упомянутые в разделе о жидкости методы, использующие многочастичные функции распределения квазичастиц, во многих отношениях близки к методам квантовой теории поля. Использование этих функций всегда основано на приближенном "расцеплении" — выражении функции более высокого порядка через функции более низкого.
Фазовые переходы. При непрерывном изменении внешних параметров (например, давления или температуры) свойства системы могут при некоторых значениях параметров измениться скачкообразно, т. е. происходит фазовый переход. Фазовые переходы делятся на переходы первого рода, сопровождающиеся выделением скрытой теплоты перехода и скачкообразным изменением объема (к ним относится, например, плавление), и переходы второго рода, в которых скрытая теплота и скачок объема отсутствуют (например, переход в сверхпроводящее состояние). Статистическая теория фазовых переходов составляет важную, но еще далекую от завершения область С Наибольшую трудность для теоретического исследования представляют при этом свойства вещества вблизи линии фазового перехода второго рода и вблизи критической точки фазового перехода первого рода. С математической точки зрения термодинамические функции системы имеют здесь особенности. Вблизи этих точек происходят своеобразные критические явления. В то же время здесь аномально возрастают флуктуации, и рассмотренные выше приближенные методы С оказываются неприменимыми. Поэтому важную роль играет небольшое число точно решаемых моделей, в которых есть переходы (например, т. н. модель Изинга).
Флуктуации. В основе С лежит тот факт, что физические величины, характеризующие макроскопические тела, с большой точностью равны своим средним значениям. Это равенство является все же приближенным, в действительности все величины испытывают малые беспорядочные отклонения от средних значений — флуктуации. Существование флуктуаций имеет большое принципиальное значение, т.к. прямо доказывает статистический характер термодинамических закономерностей. Кроме того, флуктуации играют роль шума, мешающего физическим измерениям и ограничивающего их точность. Флуктуации некоторой величины х около ее среднего значения 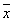 характеризуются средним квадратом флуктуации характеризуются средним квадратом флуктуации
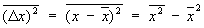 . .
В подавляющем большинстве случаев величина х испытывает флуктуации порядка , существенно большие флуктуации встречаются крайне редко. Знание функции распределения системы позволяет вычислить средний квадрат флуктуации точно так же, как и среднее значение любой физической величины. Малые флуктуации термодинамических величин можно вычислить, используя статистическое истолкование энтропии. Согласно (10), вероятность неравновесного состояния системы с энтропией пропорциональна e/k. Это приводит к формуле , существенно большие флуктуации встречаются крайне редко. Знание функции распределения системы позволяет вычислить средний квадрат флуктуации точно так же, как и среднее значение любой физической величины. Малые флуктуации термодинамических величин можно вычислить, используя статистическое истолкование энтропии. Согласно (10), вероятность неравновесного состояния системы с энтропией пропорциональна e/k. Это приводит к формуле
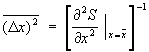 . (22) . (22)
Например, средние квадраты флуктуаций объема и температуры тела равны:
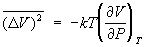 , , 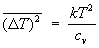 (23) (23)
Из этих формул видно, что относительные флуктуации объема и флуктуации температуры обратно пропорциональны 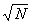 , где — число частиц в теле. Это и обеспечивает малость флуктуаций для макроскопических тел. Связь между флуктуациями различных величин xi, xk хара , где — число частиц в теле. Это и обеспечивает малость флуктуаций для макроскопических тел. Связь между флуктуациями различных величин xi, xk хара |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 12:12:12
|

|

|
 |
|

|
 |
 |
 |
|