Спирали

Спирали (далее С) (франц., единственное число spirale, от лат. spira, греч. speira - виток), плоские кривые линии, бесчисленное множество раз обходящие некоторую точку, с каждым обходом приближаясь к ней или с каждым обходом удаляясь от нее. Если выбрать эту точку за полюс полярной системы координат, то полярное уравнение С r = f(j) таково, что f(j + 2p) > f(j) или f(j + 2p) < f(j) при всех j. В частности, С получаются, если f(j) - монотонно возрастающая или убывающая положительная функция. Наиболее простой вид имеет уравнение архимедовой С (см. рис.): r = аj, изученной древнегреческим математиком Архимедом (3 в. до н. э.) в связи с задачами трисекции угла и квадратуры круга в сочинении "О спиралях". Архимед нашел площадь сектора этой С, что было одним из первых примеров квадратуры криволинейной области. Архимедова С является подерой (см. Подера и антиподера) эвольвенты круга (см. Эволюта и эвольвента), что используется в некоторых конструкциях разводных мостов для уравновешивания переменного натяжения цепи. Если эксцентрик ограничен дугами архимедовой С (сердцевидный эксцентрик), то он преобразует равномерное вращательное движение в равномерное поступательное, причем расстояние между диаметрально противоположными точками эксцентрика постоянно. Французский математик П. Ферма исследовал обобщенные архимедовы С (r/a)n = (j/2p)m и нашел площадь их сектора.   Уравнение r = аекj задает логарифмическую С (см. рис.). Логарифмическая С пересекает под одним и тем же углом а все радиус-векторы, проведенные из полюса, причем ctga = k. Это свойство логарифмической С используется при проектировании вращающихся ножей, фрез и т. д. для достижения постоянства угла резания. Логарифмическая С встречается также в теории спиральных приводов к гидравлическим турбинам и т. д. В теории зубчатых колес используется возможность качения без скольжения одной логарифмической С по другой, равной с ней, когда обе С вращаются вокруг своих полюсов. При этом получаются зубчатые передачи с переменным передаточным числом. При стереографической проекции плоскости на сферу логарифмической С переходит в локсодромию (кривую, пересекающую все меридианы под одним и тем же углом). Определение длин дуг логарифмической С дано итал. ученым Э. Торричелли. Длина дуги логарифмической С пропорциональна разности длин радиус-векторов, проведенных в концы дуги, точнее равна 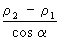. Швейц. ученый Я. Бернулли показал, что эволюта и каустика (см. Каустическая поверхность) логарифмической С являются логарифмическими С При вращении вокруг полюса логарифмической С получается кривая, гомотетичная (см. Гомотетия) исходной. При инверсии логарифмическая С переходит в логарифмическую С   Из других С практическое значение имеет Корню С (или клотоида), применяемая при графическом решении некоторых задач дифракции (см. рис.). Параметрическое уравнение этой С имеет вид: , 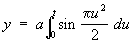.   Корню С является идеальной переходной кривой для закругления пути, так как ее радиус кривизны возрастает пропорционально длине дуги. С являются также эвольвенты замкнутых кривых, например эвольвента окружности.   Названия некоторым С даны по сходству их полярных уравнений с уравнениями кривых в декартовых координатах, например параболическая С (см. рис.): (а - r)2 = bj, гиперболическая С(см. рис.): r = а/j. К С относятся также жезл (см. 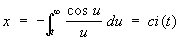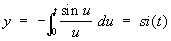рис.): r2 = a/j и si-ci-cпираль, параметрические уравнения которой имеют вид: ,   (si (t) и ci (t) - интегральный синус и интегральный косинус). Кривизна si-ci-cпирали изменяется с длиной дуги по закону показательной функции. Такие С применяют в качестве профиля для лекал.   Напоминает С кривая 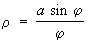, называемая кохлеоидой (см. рис.). Она бесконечное множество раз проходит через полюс, причем каждый следующий завиток лежит в предыдущем.   С встречаются также при рассмотрении особых точек в теории дифференциальных уравнений (см. Особые точки).   С иногда называют также пространственные кривые, делающие бесконечно много оборотов вокруг некоторой оси, например винтовая линия.   Лит. см. при ст. Линия.