
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Собственные функции | Собственные функции (далее С) понятие математического анализа. При решении многих задач математической физики (в теории колебаний, теплопроводности и т.д.) возникает необходимость в нахождении не равных тождественно нулю решений однородных линейных дифференциальных уравнений L (y) = lу, удовлетворяющих тем или иным краевым условиям. Такие решения называют С задачи, а соответствующие значения l — собственными значениями. Если дифференциальное уравнение с соответствующими краевыми условиями самосопряженное (см. Самосопряженное дифференциальное уравнение), то его собственные значения действительны, а С, соответствующие различным собственным значениям, ортогональны. Если дифференциальное уравнение рассматривается на конечном отрезке и его коэффициенты не имеют на этом отрезке особенностей, то множество С счетно (задача имеет дискретный спектр); знание С и соответствующих собственных значений позволяет тогда при некоторых условиях получить решение задачи в виде ряда по С (см. Фурье метод). Если же уравнение рассматривается на бесконечном промежутке или его коэффициенты имеют особенности (например, если коэффициент при старшей производной обращается в нуль), может существовать континуум С, и вместо разложения в ряд получается разложение в интеграл по С, аналогичное представлению в виде Фурье интеграла. В этом случае говорят, что задача имеет непрерывный спектр. Многие специальные функции (ортогональные многочлены и др.) служат С некоторых уравнений.
В теории интегральных уравнений С ядра К (х, у) называют функцию, удовлетворяющую при некотором значении l уравнению
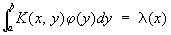 . .
Всякое симметрическое непрерывное ядро имеет С В этом случае всякая функция, представимая в виде
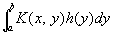 , ,
может быть разложена в ряд по С Если ядро имеет особенности или задано в бесконечной области, то может также возникнуть непрерывный спектр.
Наиболее общим образом С можно определить как собственные векторы линейных операторов в линейных функциональных пространствах. В квантовой механике С оператора, отвечающего какой-либо физической величине (см. Операторы в квантовой теории), соответствуют состояниям системы, в которых данная физическая величина имеет определенное значение.
Иногда С называют также фундаментальными функциями, характеристическими функциями и т.д.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 12:27:06
|

|

|
 |
|

|
 |
 |
 |
|