|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Синусоидальные спирали | Синусоидальные спирали (далее С) синус-спирали, кривые, уравнения которых в полярной системе координат имеют вид
 , (*)
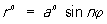где n — рациональное число. Частными случаями С являются окружность, прямая, равнобочная гипербола, лемниската, кардиоида, парабола (см. Линия)
(соответственно при n = 1, —1, —2, 2, 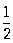 ,  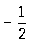). Логарифмическую спираль можно рассматривать как некоторый предельный случай С при n = 0 (хотя уравнение (*) теряет при этом смысл), разделяющей С, лежащие в конечной части плоскости, от С, имеющих бесконечные ветви. Проекция центра кривизны любой точки С на радиус-вектор этой точки делит его в отношении n: 1 (считая от полюса). При равномерном вращении радиус-вектора С вокруг полюса касательная равномерно вращается вокруг точки касания. Поэтому С называются также кривыми пропорционального изгиба. При натуральном n С состоит из n лепестков, лежащих в углах
 , 
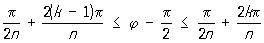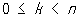
касаясь в начале координат сторон угла. Углы
 , 
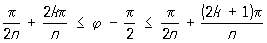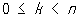
не содержат точек С, отличных от начала координат. Если вписать в круг радиуса а.2-1/n правильный n- 1, 2,..., Рп, то множество точек, произведение расстояний которых до точек 1, 2,..., Рп равно an/2, является С Площадь одного лепестка С равна
 ,
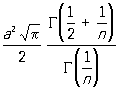а периметр равен
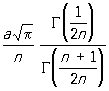
где G(х) — гамма-функция. При натуральном n С. с. имеет n осей симметрии. Если n = 1/q, то кривая симметрична относительно полярной оси, причем каждая из половин кривой имеет вид спирали, начинающейся в точке r = а, j = p/2 и после оборота на угол qp/2 приходящей в полюс. С при n = p/q является алгебраической кривой (см. Алгебраическая геометрия), обладающей р осями симметрии, наклоненными к вертикальной оси под углами 2pqk/p, 0 £ k < p. Изучение С с отрицательными значениями п сводится к изучению С с положительными п при помощи преобразования инверсии. С применяются в некоторых вопросах механики, геодезии и др.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 21.11.2024 12:09:26
|
|
|
|
|
|
|
|
|
|
|
