
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Симметрия кристаллов | Симметрия свойство (далее С) совмещаться с собой в различных положениях путем поворотов, отражений, параллельных переносов либо части или комбинации этих операций. Симметрия внешней формы (огранки) определяется симметрией его строения, которая обусловливает также и симметрию физических свойств
На рис. 1, а изображен кварца. Внешняя его форма такова, что поворотом на 120° вокруг оси 3 он может быть совмещен сам с собой (совместимое равенство). метасиликата (рис. 1, б) преобразуется в себя отражением в плоскости симметрии m (зеркальное равенство). Т. о., симметрия означает возможность преобразования объекта совмещающего его с собой. Если (x1, x2, x3) — функция, описывающая объект, например форму в трехмерном пространстве или какое-либо его свойство, а операция g (x1, x2, x3) осуществляет преобразование координат всех точек объекта, то g является операцией или преобразованием симметрии, а — симметричным объектом, если выполняются условия:
g (x1,. x2, x3) = 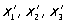 (1, a) (1, a)
(x1, x2, x3) = (x2, x2, x3). (1, б)
В наиболее общей формулировке симметрия — неизменность (инвариантность) объектов при некоторых преобразованиях описывающих их переменных. — объекты в трехмерном пространстве, поэтому классическая теория Симметрия — теория симметрических преобразований в себя трехмерного пространства с учетом того, что внутренняя структура — трехмерно-периодическая, т. е. описывается как кристаллическая решетка. При преобразованиях симметрии пространство не деформируется, а преобразуется как жесткое целое (ортогональное, или изометрическое, преобразование). После преобразования симметрии части объекта, находившиеся в одном месте, совпадают с частями, находящимися в др. месте. Это означает, что в симметричном объекте есть равные части (совместимые или зеркальные).
Симметрия проявляется не только в их структуре и свойствах в реальном трехмерном пространстве, но также и при описании энергетического спектра электронов в импульсном пространстве (см. Твердое тело), при анализе процессов дифракции рентгеновских лучей в с помощью пространства обратных длин и т. п.
Группа симметрии может быть присуща не одна, а несколько операций симметрии. Так, кварца (рис. 1, а) совмещается с собой нс только при повороте на 120° вокруг оси 3 (операция g1), ной при повороте вокруг оси 3 на 240° (операция g2), а также при поворотах на 180° вокруг осей 2x, 2y, 2w (операции g3, g4 и g5). Каждой операции симметрии может быть сопоставлен геометрический образ — элемент симметрии — прямая, плоскость или точка, относительно которой производится данная операция. Например, ось 3 или оси 2x, 2y, 2w являются осями симметрии, плоскость m (рис. 1, б) — плоскостью зеркальной симметрии и т. п. Совокупность операций симметрии (g1,..., gn) данного образует группу симметрии G в смысле математической теории групп. Последовательное проведение двух операций симметрии также является операцией симметрии. Всегда существует операция идентичности g0, ничего не изменяющая в называется отождествлением, геометрически соответствующая неподвижности объекта или повороту его на 360° вокруг любой оси. Число операций, образующих группу G, называется порядком группы.
Группы симметрии классифицируют: по числу n измерений пространства, в которых они определены; по числу т измерений пространства, в которых объект периодичен (их соответственно обозначают Gmn) и по некоторым другим признакам. Для описания используют различные группы симметрии, из которых важнейшими являются пространственные группы симметрии G33, описывающие структуру и точечные группы симметрии G03, описывающие их внешнюю форму. Последние называются также классами.
Симметрия огранки Операциями точечной симметрии являются: повороты вокруг оси симметрии порядка на 360°/ (рис. 2, а), отражение в плоскости симметрии (зеркальное отражение, рис. 2, б), инверсия 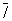 (симметрия относительно точки, рис. 2, в), инверсионные повороты (симметрия относительно точки, рис. 2, в), инверсионные повороты 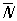 (комбинация поворота на 360°/ с одновременной инверсией, рис. 2, г). Вместо инверсионных поворотов иногда рассматривают зеркальные повороты (комбинация поворота на 360°/ с одновременной инверсией, рис. 2, г). Вместо инверсионных поворотов иногда рассматривают зеркальные повороты 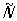 . Геометрически возможные сочетания этих операций определяют ту или иную точечную группу (рис. 3), которые изображаются обычно в стереографической проекции. При преобразованиях точечной симметрии по крайней мере одна точка объекта остается неподвижной — преобразуется сама в себя. В ней пересекаются все элементы симметрии, и она является центром стереографической проекции. . Геометрически возможные сочетания этих операций определяют ту или иную точечную группу (рис. 3), которые изображаются обычно в стереографической проекции. При преобразованиях точечной симметрии по крайней мере одна точка объекта остается неподвижной — преобразуется сама в себя. В ней пересекаются все элементы симметрии, и она является центром стереографической проекции.
Точечные преобразования симметрии g (x1, x2, x3) = 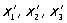 описываются линейными уравнениями: описываются линейными уравнениями:
x"1 = а11х1 + a12x2 + a13x3,
x"2 = a21x1 + a22x2 + a23x3, (2)
x"3 = a31x1 + a32x2 + a33x3,
т. е. матрицей коэффициента (aij). Например, при повороте вокруг хз на угол a = 360°/ матрица коэффициентов имеет вид:
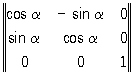 , (3) , (3)
а при отражении в плоскости x1, x2 имеет вид:
 (3a) (3a)
Поскольку может быть любым, число групп 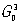 бесконечно. Однако в ввиду наличия решетки возможны только операции и соответственно оси симметрии до 6-го порядка (кроме 5-го), которые обозначаются символами: 1, 2, 3, 4, 6, а также инверсионные оси: бесконечно. Однако в ввиду наличия решетки возможны только операции и соответственно оси симметрии до 6-го порядка (кроме 5-го), которые обозначаются символами: 1, 2, 3, 4, 6, а также инверсионные оси: 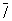 (она же центр симметрии), (она же центр симметрии), 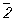 = m (она же плоскость симметрии), = m (она же плоскость симметрии), 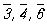 . Поэтому количество точечных групп, описывающих внешнюю форму ограничено. Эти 32 группы Симметрия приведены в таблице. В международные обозначения точечных групп входят символы основных (порождающих) элементов симметрии, им присущих. Эти группы объединяются по симметрии формы элементарной ячейки (с периодами а, b, с и углами a, b, g) в 7 сингоний кристаллографических — триклинную, моноклинную, ромбическую, тетрагональную, тригональную, гексагональную и кубическую. Принадлежность к той или иной группе определяется гониометрически (см. Гониометр) или рентгенографически (см. Рентгеновский структурный анализ). . Поэтому количество точечных групп, описывающих внешнюю форму ограничено. Эти 32 группы Симметрия приведены в таблице. В международные обозначения точечных групп входят символы основных (порождающих) элементов симметрии, им присущих. Эти группы объединяются по симметрии формы элементарной ячейки (с периодами а, b, с и углами a, b, g) в 7 сингоний кристаллографических — триклинную, моноклинную, ромбическую, тетрагональную, тригональную, гексагональную и кубическую. Принадлежность к той или иной группе определяется гониометрически (см. Гониометр) или рентгенографически (см. Рентгеновский структурный анализ).
Группы, содержащие лишь повороты, описывают состоящие только из совместимо равных частей. Эти группы называются группами 1-го рода. Группы, содержащие отражения, или инверсионные повороты, описывают в которых есть зеркально равные части (но могут быть и совместимо равные части). Эти группы называются группами 2-го рода. описываемые группами 1-го рода, могут в двух энантиоморфных формах, условно называемых "правой" и "левой", каждая из них не содержит элементов симметрии 2-го рода, но они зеркально равны друг другу (см. Энантиоморфизм, Кварц).
Точечные группы описывают симметрию не только но любых конечных фигур. В живой природе часто наблюдается запрещенная в симметрия с осями 5-го, 7-го порядка и выше. Например, для описания регулярной структуры сферических вирусов (рис. 4), в оболочках которых соблюдаются принципы плотной укладки молекул, оказалась важной икосаэдрическая точечная группа 532.
Симметрия физических свойств. Предельные группы. В отношении макроскопических физических свойств (оптических, электрических, механических и др.), ведут себя как однородная анизотропная среда, т. е. дискретность их структуры не проявляется. Однородность означает, что свойства одинаковы в любой точке однако при этом многие свойства зависят от направления (см. Анизотропия). Зависимость от направления можно представить в виде функции и построить указательную поверхность данного свойства (рис. 5, см. также ст. Кристаллооптика). Эта функция, которая может быть различной для разных физических свойств (векторной или тензорной) имеет определенную точечную симметрию, однозначно связанную с группой симметрии огранения Она либо совпадает с ней, либо выше ее по симметрии (принцип Неймана).
Многие из свойств принадлежащих к определенным классам, описываются предельными точечными группами, содержащими оси симметрии бесконечного порядка, обозначаемые ¥. Наличие оси ¥ означает, что объект совмещается с собой при повороте на любой, в том числе бесконечно малый угол. Таких групп 7, они представлены на рис. 6 образцовыми фигурами и соответствующими символами. Т. о., всего имеется 32 + 7 = 39 точечных групп, описывающих симметрию свойств Зная группу Симметрия можно указать возможность наличия или отсутствия в нем некоторых физических свойств (см. Кристаллы, Кристаллофизика).
Обозначения и названия 32 групп точечной симметрии<
Сингония
|
Обозначения
| Название |
Соотношение констант эле-
ментарной ячейки
|
международные
|
по Шенфлису
|
Триклинная
|
|
С1
|
Моноэдрическая
|
а ¹ b ¹ с
|
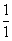
|
С1
|
Пинакоидальная
|
a ¹ b ¹ g ¹ 90°
|
Моноклинная
|
2
|
С2
|
Диэдрическая осевая
|
а ¹ b ¹ с
|
m
|
|
Диэдрическая безосная
|
a = g = 90°
|
2/m
|
2h
|
Призматическая
|
b ¹ 90°
|
Ромбическая
|
222
|
D2
|
Ромбо-тетраэдрическая
|
а ¹ b ¹ с
|
mm
|
2u
|
Ромбо-пирамидальная
|
|
mmm
|
D2h
|
Ромбо-дипирамидальная
|
a = b = g = 90°
|
Тетрагональная
|
4
|
4
|
Тетрагонально-пирамидальная
|
а = b ¹ с
a = b = g = 90°
|
422
|
D4
|
Тетрагонально-трапецоэдрическая
|
4/m
|
4h
|
Тетрагонально-дипирамидальная
|
4mm
|
4u
|
Дитетрагонально-пирамидальная
|
4/mmm
|
D4h
|
Дитетрагонально-дипирамидальная
|
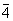
|
4
|
Тетрагонально-тетраэдрическая
|
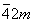
|
D2d
|
Тетрагонально-скаленоэдрическая
|
Тригональная
|
3
|
3
|
Тригонально-пирамидальная
|
а = b = с
a = b = g ¹ 90°
|
32
|
D3
|
Тригонально-трапецоэдрическая
|
3m
|
3u
|
Дитригонально-пирамидальная
|
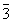
|
3i
|
Ромбоэдрическая
|
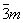
|
D3d
|
Дитригонально-скаленоэдрическая
|
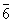
|
3h
|
Тригонально-дипирамидальная
|
Гексагональная
|
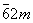
|
D3h
|
Дитригонально-дипирамидальная
|
а = b ¹ с
a = b = 90°
g = 120°
|
6
|
6
|
Гексагонально-пирамидальная
|
62
|
D6
|
Гексагонально-трапецоэдрическая
|
6/m
|
6h
|
Гексагонально-дипирамидальная
|
6mm
|
6u
|
Дигексагонально-пирамидальная
|
6/mmm
|
D6h
|
Дигексагонально-дипирамидальная
|
Кубическая
|
23
|
T
|
Тритетраэдрическая
|
а = b = с
a = b = g = 90°
|
m3
|
Th
|
Дидодекаэдрическая
|
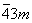
|
Td
|
Гексатетраэдрическая
|
43
|
|
Триоктаэдрическая
|
m3m
|
Oh
|
Гексоктаэдрическая
|
Пространственная симметрия структуры ( решетки) описывается пространственными группами симметрии 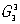 . Характерными для решетки операциями являются три некомпланарных переноса а, b, с, называемых трансляциями, которые задают трехмерную периодичность структуры Сдвиг (перенос) структуры на векторы a1, b2, c3 или любой вектор t = p1a1 + p2b2 + p3c3, где p1, p2, p3 — любые целые положительные или отрицательные числа, совмещает структуру с собой, и следовательно, является операцией симметрии, удовлетворяющей условиям (1, а, б). Параллелепипед, построенный на векторах а, b и c, называется параллелепипедом повторяемости или элементарной ячейкой (рис. 7, а, б). В элементарной ячейке содержится некоторая минимальная группировка "размножение" которой операциями симметрии, в том числе трансляциями, образует решетку. Элементарная ячейка и размещение в ней устанавливается методами рентгеновского структурного анализа, электронографии или нейтронографии. . Характерными для решетки операциями являются три некомпланарных переноса а, b, с, называемых трансляциями, которые задают трехмерную периодичность структуры Сдвиг (перенос) структуры на векторы a1, b2, c3 или любой вектор t = p1a1 + p2b2 + p3c3, где p1, p2, p3 — любые целые положительные или отрицательные числа, совмещает структуру с собой, и следовательно, является операцией симметрии, удовлетворяющей условиям (1, а, б). Параллелепипед, построенный на векторах а, b и c, называется параллелепипедом повторяемости или элементарной ячейкой (рис. 7, а, б). В элементарной ячейке содержится некоторая минимальная группировка "размножение" которой операциями симметрии, в том числе трансляциями, образует решетку. Элементарная ячейка и размещение в ней устанавливается методами рентгеновского структурного анализа, электронографии или нейтронографии.
Вследствие возможности комбинирования в решетке трансляций и операций точечной симметрии в группах G33 возникают операции и соответствующие им элементы симметрии с трансляционной компонентой — винтовые оси различных порядков и плоскости скользящего отражения (рис. 2, д).
Всего известно 230 пространственных (федоровских) групп симметрии 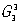 , и любой относится к одной из этих групп. Трансляционные компоненты элементов микросимметрии макроскопически не проявляются, например винтовая ось в огранке проявляется как соответствующая по порядку простая поворотная ось. Поэтому каждая из 230 групп , и любой относится к одной из этих групп. Трансляционные компоненты элементов микросимметрии макроскопически не проявляются, например винтовая ось в огранке проявляется как соответствующая по порядку простая поворотная ось. Поэтому каждая из 230 групп 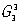 макроскопически сходственна с одной из 32 точечных групп. Например, точечной группе mmm или D2h сходственны 28 пространственных групп. Совокупность переносов, присущих данной пространственной группе, есть ее трансляционная подгруппа, или Браве решетка; таких решеток существует 14. макроскопически сходственна с одной из 32 точечных групп. Например, точечной группе mmm или D2h сходственны 28 пространственных групп. Совокупность переносов, присущих данной пространственной группе, есть ее трансляционная подгруппа, или Браве решетка; таких решеток существует 14.
Симметрия слоев и цепей. Для описания плоских или вытянутых в одном направлении фрагментов структуры могут быть использованы группы 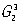 — двумерно периодические и — двумерно периодические и 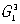 — одномерно периодические в трехмерном пространстве. Эти группы играют важную роль в изучении биологических структур и молекул. Например, группы — одномерно периодические в трехмерном пространстве. Эти группы играют важную роль в изучении биологических структур и молекул. Например, группы 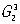 описывают строение биологических мембран, группы описывают строение биологических мембран, группы 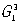 — цепных молекул (рис. 8, а) палочкообразных вирусов, трубчатых глобулярных белков (рис. 8, б), в которых молекулы уложены согласно спиральной (винтовой) симметрии, возможной в группах — цепных молекул (рис. 8, а) палочкообразных вирусов, трубчатых глобулярных белков (рис. 8, б), в которых молекулы уложены согласно спиральной (винтовой) симметрии, возможной в группах 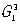 . .
Обобщенная симметрия. В основе определения симметрии лежит понятие равенства (1, б) при преобразовании (1, а). Однако физически (и математически) объект может быть равен себе по одним признакам и не равен по другим. Например, распределение ядер и электронов в антиферромагнетика можно описать с помощью обычной пространственной симметрии, но если учесть распределение в нем моментов (рис. 9), то "обычной", классической симметрии уже недостаточно. К подобного рода обобщениям симметрии относится антисимметрия и цветная симметрия. В антисимметрии в дополнение к трем пространственным переменным x1, x2, x3 вводится добавочная, 4-я переменная x4 = ± 1. Это можно истолковать таким образом, что при преобразовании (1, а) функция может быть не только равна себе, как в (1, б), но и изменить знак. Условно такую операцию можно изобразить изменением цвета (рис. 10). Существует 58 групп точечной антисимметрии 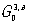 и 1651 пространственная группа антисимметрии и 1651 пространственная группа антисимметрии 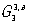 (шубниковских групп). Если добавочная переменная приобретает не два значения, а несколько (возможны числа 3, 4, 6, 8,..., 48), то возникает "цветная" симметрия Белова. Так, известна 81 точечная группа G03, ц. Основные приложения обобщенной симметрии в — описание структур. (шубниковских групп). Если добавочная переменная приобретает не два значения, а несколько (возможны числа 3, 4, 6, 8,..., 48), то возникает "цветная" симметрия Белова. Так, известна 81 точечная группа G03, ц. Основные приложения обобщенной симметрии в — описание структур.
Др. обобщения симметрии: симметрия подобия, когда равенство частей фигуры заменяется их подобием (рис. 11), криволинейная симметрия, статистическая симметрия, вводимая при описании структуры разупорядоченных твердых растворов, жидких кристаллов, и др.
Лит.: Шубников А. В., Копцик В. А., Симметрия в науке и искусстве, 2 изд., М., 1972; Вейль Г., Симметрия, пер. с англ., М., 1968; Федоров Е. С.. Симметрия и структура (М.), 1949; Шубников А. В., Симметрия и антисимметрия конечных фигур, М., 1951.
Б. К. Вайнштейн.
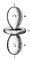
Рис. 5. Поверхность, описывающая оптическую активность кристалла кварца; знаки (+) и (-) указывают противоположные направления вращения плоскости поляризации.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 11:40:09
|

|

|
 |
|

|
 |
 |
 |
|