
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Симметрические функции | Симметрические функции (далее С)функции нескольких переменных, не изменяющиеся при любых перестановках переменных, например 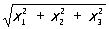 или или 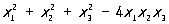 . Особое значение в алгебре имеют симметрические многочлены (с. м.) и среди них — элементарные симметрические многочлены (э. с. м.) — функции . Особое значение в алгебре имеют симметрические многочлены (с. м.) и среди них — элементарные симметрические многочлены (э. с. м.) — функции
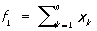 , , 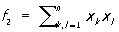 , , 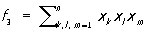 , …, , …, 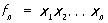 , ,
где суммы распространены на комбинации неравных между собой чисел k, l,...; они имеют первую степень относительно каждого из переменных. Согласно формулам Виета, x1, x2,..., xn являются корнями уравнения:
xn - f1xn-1 + f2xn-2 - ··· + (- 1) nfn = 0.
Согласно основной теореме теории Симметрические функции, любой с. м. представляется как многочлен от э. с. м., и притом только единственным образом: (x1, x2.,..., xn) = G (f1, f2,..., fn); если все коэффициенты в целые, то и коэффициенты в G целые. Иными словами, всякий с. м. от корней уравнения выражается целым рациональным образом через его коэффициенты; например,
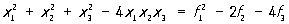 . .
Другим важным классом Симметрические функции являются степенные суммы
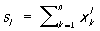 . .
Они связаны с э. с. м. формулами Ньютона
si - f1sl-1 + f2sl-2 + ··· + (— 1) lfl = 0, 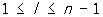 , ,
и
sn+l - f1sn+l-1 + ··· +(-1) n fnsl = 0,
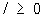 , ,
позволяющими последовательно выражать fk через srn и обратно.
Функция называется кососимметрической, или знакопеременной, если она не изменяется при четных перестановках x1, x2,..., xn и меняет знак при нечетных перестановках. Такие функции рационально выражаются через f1, f2,..., fn и разностное произведение (см. Дискриминант) D = Пк<1 (xk — xl), квадрат которого является Симметрические функции и потому рационально выражается через f1, f2,..., fn.
Лит.: Курош А. Г., Курс высшей алгебры, 10 изд., М., 1971. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|