
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Самосопряженная матрица | Самосопряженная матрица (далее С)(математическая), матрица, совпадающая со своей сопряженной, т. е. такая, что aik = 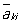 , где , где 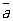 - число, комплексно сопряженное с а. Если элементы Самосопряженная матрица действительны, то она симметрическая (см. Симметрическая матрица). Самосопряженная матрица имеет действительные собственные значения l1, l2,..., ln и соответствует линейному преобразованию в комплексном n-мерном пространстве, сводящемуся к растяжениям в |li| раз по n взаимно перпендикулярным направлениям и зеркальным отражениям в плоскостях, ортогональных тем из этих направлений, для которых li < 0. Билинейную форму вида - число, комплексно сопряженное с а. Если элементы Самосопряженная матрица действительны, то она симметрическая (см. Симметрическая матрица). Самосопряженная матрица имеет действительные собственные значения l1, l2,..., ln и соответствует линейному преобразованию в комплексном n-мерном пространстве, сводящемуся к растяжениям в |li| раз по n взаимно перпендикулярным направлениям и зеркальным отражениям в плоскостях, ортогональных тем из этих направлений, для которых li < 0. Билинейную форму вида 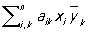 , коэффициенты которой образуют Самосопряженная матрица, называют эрмитовой формой. Всякая матрица может быть записана в виде A1 + iA2, где A1 и A2 суть Самосопряженная матрица, а также в виде AU, где А является Самосопряженная матрица, a - унитарная матрица. Если А и В суть Самосопряженная матрица, то AB является Самосопряженная матрица тогда и только тогда, когда А и В перестановочны. , коэффициенты которой образуют Самосопряженная матрица, называют эрмитовой формой. Всякая матрица может быть записана в виде A1 + iA2, где A1 и A2 суть Самосопряженная матрица, а также в виде AU, где А является Самосопряженная матрица, a - унитарная матрица. Если А и В суть Самосопряженная матрица, то AB является Самосопряженная матрица тогда и только тогда, когда А и В перестановочны.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 12:00:36
|

|

|
 |
|

|
 |
 |
 |
|