
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Резонанс | Резонанс (далее Р) (франц. resonance, от лат. resono — звучу в ответ, откликаюсь), явление резкого возрастания амплитуды вынужденных колебаний в какой-либо колебательной системе, наступающее при приближении частоты периодического внешнего воздействия к некоторым значениям, определяемым свойствами самой системы. В простейших случаях Р наступает при приближении частоты внешнего воздействия к одной из тех частот, с которыми происходят собственные колебания в системе, возникающие в результате начального толчка. Характер явления Р существенно зависит от свойств колебательной системы. Наиболее просто Р протекает в тех случаях, когда периодическому воздействию подвергается система с параметрами, не зависящими от состояния самой системы (т. н. линейные системы).
Типичные черты Р можно выяснить, рассматривая случай гармонического воздействия на систему с одной степенью свободы: например, на массу m, подвешенную на пружине, находящуюся под действием гармонической силы = 0 coswt (рис. 1), или электрическую цепь, состоящую из последовательно соединенных индуктивности L, емкости С, сопротивления R и источника электродвижущей силы Е, меняющейся по гармоническому закону (рис. 2). Для определенности в дальнейшем рассматривается первая из этих моделей, но все сказанное ниже можно распространить и на вторую модель. Примем, что пружина подчиняется закону Гука (это предположение необходимо, чтобы система была линейна), т. е., что сила, действующая со стороны пружины на массу m, равна kx, где х — смещение массы от положения равновесия, k — коэффициент упругости (сила тяжести для простоты не принимается во внимание). Далее, пусть при движении масса испытывает со стороны окружающей среды сопротивление, пропорциональное ее скорости 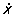 и коэффициенту трения b, т. е. равное k и коэффициенту трения b, т. е. равное k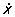 (это необходимо, чтобы система оставалась линейной). Тогда уравнение движения массы m при наличии гармонической внешней силы имеет вид: (это необходимо, чтобы система оставалась линейной). Тогда уравнение движения массы m при наличии гармонической внешней силы имеет вид:
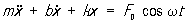 (1) (1)
где 0 — амплитуда колебания, w — циклическая частота, равная 2p/Т, Т — период внешнего воздействия, 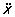 — ускорение массы m. Решение этого уравнения может быть представлено в виде суммы двух решений. Первое из этих решений соответствует свободным колебаниям системы, возникающим под действием начального толчка, а второе — вынужденным колебаниям. Собственные колебания в системе вследствие наличия трения и сопротивления среды всегда затухают, поэтому по истечении достаточного промежутка времени (тем большего, чем меньше затухание собственных колебаний) в системе останутся одни только вынужденные колебания. Решение, соответствующее вынужденным колебаниям, имеет вид: — ускорение массы m. Решение этого уравнения может быть представлено в виде суммы двух решений. Первое из этих решений соответствует свободным колебаниям системы, возникающим под действием начального толчка, а второе — вынужденным колебаниям. Собственные колебания в системе вследствие наличия трения и сопротивления среды всегда затухают, поэтому по истечении достаточного промежутка времени (тем большего, чем меньше затухание собственных колебаний) в системе останутся одни только вынужденные колебания. Решение, соответствующее вынужденным колебаниям, имеет вид:
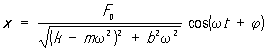 , (2) , (2)
причем tgj = 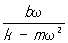 . Т. о., вынужденные колебания представляют собой гармонические колебания с частотой, равной частоте внешнего воздействия; амплитуда и фаза вынужденных колебаний зависят от соотношения между частотой внешнего воздействия и параметрами системы. . Т. о., вынужденные колебания представляют собой гармонические колебания с частотой, равной частоте внешнего воздействия; амплитуда и фаза вынужденных колебаний зависят от соотношения между частотой внешнего воздействия и параметрами системы.
Зависимость амплитуды смещений при вынужденных колебаниях от соотношения между величинами массы m и упругости k легче всего проследить, полагая, что m и k остаются неизменными, а изменяется частота внешнего воздействия. При очень медленном воздействии (w ® 0) амплитуда смещений x0 " 0/k. С увеличением частоты w амплитуда x0 растет, т. к. знаменатель в выражении (2) уменьшается. Когда w приближается к значению 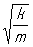 (т. е. к значению частоты собственных колебаний при малом их затухании), амплитуда вынужденных колебаний достигает максимума — наступает Р Далее с увеличением w амплитуда колебаний монотонно убывает и при w ® ¥ стремится к нулю. (т. е. к значению частоты собственных колебаний при малом их затухании), амплитуда вынужденных колебаний достигает максимума — наступает Р Далее с увеличением w амплитуда колебаний монотонно убывает и при w ® ¥ стремится к нулю.
Амплитуду колебаний при Р можно приближенно определить, полагая w = 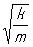 . Тогда x0 = 0/bw, т. е. амплитуда колебаний при Р тем больше, чем меньше затухание b в системе (рис. 3). Наоборот, при увеличении затухания системы Р становится все менее резким, и если b очень велико, то Р вообще перестает быть заметным. С энергетической точки зрения Р объясняется тем, что между внешней силой и вынужденными колебаниями устанавливаются такие фазовые соотношения, при которых в систему поступает наибольшая мощность (т. к. скорость системы оказывается в фазе с внешней силой и создаются наиболее благоприятные условия для возбуждения вынужденных колебаний). . Тогда x0 = 0/bw, т. е. амплитуда колебаний при Р тем больше, чем меньше затухание b в системе (рис. 3). Наоборот, при увеличении затухания системы Р становится все менее резким, и если b очень велико, то Р вообще перестает быть заметным. С энергетической точки зрения Р объясняется тем, что между внешней силой и вынужденными колебаниями устанавливаются такие фазовые соотношения, при которых в систему поступает наибольшая мощность (т. к. скорость системы оказывается в фазе с внешней силой и создаются наиболее благоприятные условия для возбуждения вынужденных колебаний).
Если на линейную систему действует периодическое, но не гармоническое внешнее воздействие, то Р наступит только тогда, когда во внешнем воздействии содержатся гармонические составляющие с частотой, близкой к собственной частоте системы. При этом для каждой отдельной составляющей явление будет протекать так же, как рассмотрено выше. А если этих гармонических составляющих с частотами, близкими к собственной частоте системы, будет несколько, то каждая из них будет вызывать резонансные явления, и общий эффект, согласно суперпозиции принципу, будет равен сумме эффектов от отдельных гармонических воздействий. Если же во внешнем воздействии не содержится гармонических составляющих с частотами, близкими к собственной частоте системы, то Р вообще не наступает. Т. о., линейная система отзывается, "резонирует" только на гармонические внешние воздействия.
В электрических колебательных системах, состоящих из последовательно соединенных емкости С и индуктивности L (рис. 2), Р состоит в том, что при приближении частот внешней эдс к собственной частоте колебательной системы, амплитуды эдс на катушке и напряжения на конденсаторе порознь оказываются гораздо больше амплитуды эдс, создаваемой источником, однако они равны по величине и противоположны по фазе. В случае воздействия гармонической эдс на цепь, состоящую из параллельно включенных емкости и индуктивности (рис. 4), имеет место особый случай Р (антирезонанс). При приближении частоты внешней эдс к собственной частоте контура LC происходит не возрастание амплитуды вынужденных колебаний в контуре, а наоборот, резкое уменьшение амплитуды силы тока во внешней цепи, питающей контур. В электротехнике это явление называется Р токов или параллельным Р Это явление объясняется тем, что при частоте внешнего воздействия, близкой к собственной частоте контура, реактивные сопротивления обеих параллельных ветвей (емкостной и индуктивной) оказываются одинаковыми по величине и поэтому в обеих ветвях контура текут токи примерно одинаковой амплитуды, но почти противоположные по фазе. Вследствие этого амплитуда тока во внешней цепи (равного алгебраической сумме токов в отдельных ветвях) оказывается гораздо меньшей, чем амплитуды тока в отдельных ветвях, которые при параллельном Р достигают наибольшей величины. Параллельный Р, так же как и последовательный Р, выражается тем резче, чем меньше активное сопротивление ветвей контура Р Последовательный и параллельный Р называются соответственно Р напряжений и Р токов.
В линейной системе с двумя степенями свободы, в частности в двух связанных системах (например, в двух связанных электрических контурах; рис. 5), явление Р сохраняет указанные выше основные черты. Однако, т. к. в системе с двумя степенями свободы собственные колебания могут происходить с двумя различными частотами (т. н. нормальные частоты, см. Нормальные колебания), то Р наступает при совпадении частоты гармонического внешнего воздействия как с одной, так и с другой нормальной частотой системы. Поэтому, если нормальные частоты системы не очень близки друг к другу, то при плавном изменении частоты внешнего воздействия наблюдаются два максимума амплитуды вынужденных колебаний (рис. 6). Но если нормальные частоты системы близки друг к другу и затухание в системе достаточно велико, так что Р на каждой из нормальных частот "тупой", то может случиться, что оба максимума сольются. В этом случае кривая Р для системы с двумя степенями свободы теряет свой "двугорбый" характер и по внешнему виду лишь незначительно отличается от кривой Р для линейного контура с одной степенью свободы. Т. о., в системе с двумя степенями свободы форма кривой Р зависит не только от затухания контура (как в случае системы с одной степенью свободы), но и от степени связи между контурами.
В связанных системах также существует явление, которое в известной мере аналогично явлению антирезонанса в системе с одной степенью свободы. Если в случае двух связанных контуров с различными собственными частотами настроить вторичный контур L22 на частоту внешней эдс, включенной в первичный контур L11 (рис. 5), то сила тока в первичном контуре резко падает и тем резче, чем меньше затухание контуров. Объясняется это явление тем, что при настройке вторичного контура на частоту внешней эдс в этом контуре возникает как раз такой ток, который в первичном контуре наводит эдс индукции, примерно равную внешней эдс по амплитуде и противоположную ей по фазе.
В линейных системах со многими степенями свободы и в сплошных системах Р сохраняет те же основные черты, что и в системе с двумя степенями свободы. Однако в этом случае, в отличие от систем с одной степенью свободы, существенную роль играет распределение внешнего воздействия по отдельным координатам. При этом возможны такие специальные случаи распределения внешнего воздействия, при которых, несмотря на совпадения частоты внешнего воздействия с одной из нормальных частот системы, Р все же не наступает. С энергетической точки зрения это объясняется тем, что между внешней силой и вынужденными колебаниями устанавливаются такие фазовые соотношения, при которых мощность, поступающая в систему от источника возбуждения по одной координате, равна мощности, отдаваемой системой источнику по другой координате. Пример этого — возбуждение вынужденных колебаний в струне, когда внешняя сила, совпадающая по частоте с одной из нормальных частот струны, приложена в точке, которая соответствует узлу скоростей для данного нормального колебания (например, сила, совпадающая по частоте с основным тоном струны, приложена у самого конца струны). При этих условиях (вследствие того, что внешняя сила приложена к неподвижной точке струны) эта сила не совершает работы, мощность от источника внешней силы в систему не поступает и сколько-нибудь заметного возбуждения колебаний струны не возникает, т. е. Р не наблюдается.
Р в колебательных системах, параметры которых зависят от состояния системы, т. е. в нелинейных системах, имеет более сложный характер, чем в системах линейных. Кривые Р в нелинейных системах могут стать резко несимметричными, и явление Р может наблюдаться при различных соотношениях частот воздействия и частот собственных малых колебаний системы (т. н. дробный, кратный и комбинационный Р). Примером Р в нелинейных системах может служить т. н. феррорезонанс, т. е. резонанс в электрической цепи, содержащей индуктивность с ферромагнитным сердечником, или ферромагнитный резонанс, представляющий собой явление, связанное с Р элементарных ( вещества при приложении высокочастотного поля (см. Радиоспектроскопия).
Если внешнее воздействие производит периодические изменение энергоемких параметров колебательной системы (например, емкости в электрическом контуре), то при определенных соотношениях частот изменения параметра и собственной частоты свободных колебаний системы возможно параметрическое возбуждение колебаний, или параметрический Р
Р весьма часто наблюдается в природе и играет огромную роль в технике. Большинство сооружений и машин способны совершать собственные колебания, поэтому периодические внешние воздействия могут вызвать их Р; например Р моста под действием периодических толчков при прохождении поезда по стыкам рельсов, Р фундамента сооружения или самой машины под действием не вполне уравновешенных вращающихся частей машин и т. д. Известны случаи, когда целые корабли входили в Р при определенных числах оборотов гребного вала. Во всех случаях Р приводит к резкому увеличению амплитуды вынужденных колебаний всей конструкции и может привести даже к разрушению сооружения. Это вредная роль Р, и для устранения его подбирают свойства системы так, чтобы ее нормальные частоты были далеки от возможных частот внешнего воздействия, либо используют в том или ином виде явление антирезонанса (применяют т. н. поглотители колебаний, или успокоители). В др. случаях Р играет положительную роль, например: в радиотехнике Р — почти единственный метод, позволяющий отделить сигналы одной (нужной) радиостанции от сигналов всех остальных (мешающих) станций.
Лит.: Стрелков С. П., Введение в теорию колебаний, 2 изд., М., 1964; Горелик Г. С., Колебания и волны, Введение в акустику, радиофизику и оптику 2 изд. М., 1959.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 13:24:55
|

|

|
 |
|

|
 |
 |
 |
|