
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Пуассона интеграл | Пуассона интеграл (далее П) 1) интеграл вида
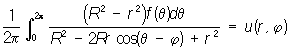 , ,
где r и j - полярные координаты, q - параметр, меняющийся на отрезке (0; 2p); П выражает значения функции u (r, j), гармонической внутри круга радиуса R, через ее значения f (q), заданные на границе этого круга. Функция u (r, j) является решением задачи Дирихле для круга (см. Гармонические функции). П был впервые рассмотрен С. Д. Пуассоном (1823). Строгая теория П была создана Г. Шварцем (1869).
2) Интеграл
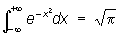 ; ;
встречается в теории вероятностей и некоторых задачах математической физики. С. Д. Пуассон предложил весьма простой прием для вычисления этого интеграла. Впервые же этот интеграл был вычислен (1729) Л. Эйлером, поэтому называется также интегралом Эйлера - Пуассона.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 12:17:49
|

|

|
 |
|

|
 |
 |
 |
|