
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Приближенные формулы | Приближенные формулы (далее П) математические формулы, получаемые из формул вида f (x) = f*(x) + e(х), где e(х) рассматривается как погрешность и после оценки отбрасывается. Таким образом, П имеет вид f (x) " f*(x).
Например, П (1 + х)2 " 1 + 2x получается из точной формулы для (1 + х)2 при малых |x|; этой формулой можно пользоваться при вычислении с точностью до сотых, тысячных, десятитысячных, если |x| соответственно не больше 0,0707..., 0,0223..., 0,00707... Эта П дает результат тем более точный, чем х ближе к 0. Но так бывает не всегда. Например, точность П tg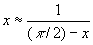 тем больше, чем х ближе к p/2. тем больше, чем х ближе к p/2.
Выше (стр. 555) приведено несколько наиболее употребительных П, причем показано, какого числа не должно превосходить |x|, чтобы формула давала k точных десятичных знаков.
Часто П получают с помощью разложения функций в ряды, например в ряд Тейлора. Чтобы уверенно применять П, необходимо иметь оценку разности между точным и приближенным выражениями функции. Зная, например, что разность между sinx и двучленом 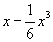 не превосходит по абсолютному значению не превосходит по абсолютному значению 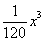 , легко убедиться, что П , легко убедиться, что П 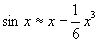 дает значения sinx с точностью до сотых, тысячных, десятитысячных, если х соответственно меньше 0,89 (51°), 0,55 (32°), 0,34 (20°). дает значения sinx с точностью до сотых, тысячных, десятитысячных, если х соответственно меньше 0,89 (51°), 0,55 (32°), 0,34 (20°). |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.11.2024 03:32:23
|

|

|
 |
|

|
 |
 |
 |
|