
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Переменный ток | Переменный ток (далее П) в широком смысле электрический ток, изменяющийся во времени. Обычно в технике под П понимают периодический ток, в котором среднее значение за период силы тока и напряжения равно нулю. Периодом Т П называют наименьший промежуток времени (выраженный в сек), через который изменения силы тока (и напряжения) повторяются (рис. 1). Важной характеристикой П является его частота f - число периодов в 1 сек: f = 1/Т. В электроэнергетических системах СССР и большинства стран мира принята стандартная частота f = 50 гц, в США - 60 гц. В технике связи применяются П высокой частоты (от 100 кгц до 30 Ггц). Для специальных целей в промышленности, медицине и др. отраслях науки и техники используют П. т, самых различных частот, а также импульсные токи (см. Импульсная техника).
Для передачи и распределения электрической энергии преимущественно используется П благодаря простоте трансформации его напряжения почти без потерь мощности (см. Передача электроэнергии, Электрическая цепь). Широко применяются трехфазные системы П (см. Трехфазная цепь). Генераторы и двигатели П по сравнению с машинами постоянного тока при равной мощности меньше по габаритам, проще по устройству, надежнее и дешевле. П может быть выпрямлен, например полупроводниковыми выпрямителями, а затем с помощью полупроводниковых инверторов преобразован вновь в П другой, регулируемой частоты; это создает возможность использовать простые и дешевые безколлекторные двигатели П (асинхронные и синхронные) для всех видов электроприводов, требующих плавного регулирования скорости.
П широко применяется в устройствах связи (радио, телевидение, проволочная телефония на дальние расстояния и т. п.).
П создается переменным напряжением. Переменное электромагнитное поле, возникающее в пространстве, окружающем проводники с током, вызывает колебания энергии в цепи П: энергия периодически то накапливается в или электрическом поле, то возвращается источнику электроэнергии. Колебания энергии создают в цепи П реактивные токи, бесполезно загружающие провода и источник тока и вызывающие дополнительные потери энергии, что является недостатком передачи энергии П
За основу для характеристики силы П принято сопоставление среднего теплового действия П с тепловым действием постоянного тока соответствующей силы. Полученное таким путем значение силы П называется действующим (или эффективным) значением, математически представляющим среднеквадратичное за период значение силы тока. Аналогично определяется и действующее значение напряжения П . Амперметры и вольтметры П измеряют именно действующие значения тока и напряжения.
В простейшем и наиболее важном на практике случае мгновенное значение силы i П меняется во времени t по синусоидальному закону: i = m sin (wt + a), где m - амплитуда тока, w = 2pf - его угловая частота, a - начальная фаза. Синусоидальный (гармонический) ток создается синусоидальным напряжением той же частоты: u = m sin (wt + b), где m - амплитуда напряжения, b - начальная фаза (рис. 2). Действующие значения такого П равны: = lm/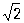 " 0,707 m, = m/ " 0,707 m, = m/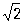 " 0,707 m. Для синусоидальных токов, удовлетворяющих условию квазистационарности (см. Квазистационарный ток; в дальнейшем будут рассматриваться только такие токи), справедлив Ома закон (закон Ома в дифференциальной форме справедлив и для неквазистационарных токов в линейных цепях). Из-за наличия в цепи П индуктивности или (и) емкости между током i и напряжением u в общем случае возникает сдвиг фаз j = b - a, зависящий от параметров цепи (активного сопротивления r, индуктивности L, емкости С) и угловой частоты w. Вследствие сдвига фаз средняя мощность Р Т. т., измеряемая ваттметром, меньше произведений действующих значений тока и напряжения: Р = cosj. " 0,707 m. Для синусоидальных токов, удовлетворяющих условию квазистационарности (см. Квазистационарный ток; в дальнейшем будут рассматриваться только такие токи), справедлив Ома закон (закон Ома в дифференциальной форме справедлив и для неквазистационарных токов в линейных цепях). Из-за наличия в цепи П индуктивности или (и) емкости между током i и напряжением u в общем случае возникает сдвиг фаз j = b - a, зависящий от параметров цепи (активного сопротивления r, индуктивности L, емкости С) и угловой частоты w. Вследствие сдвига фаз средняя мощность Р Т. т., измеряемая ваттметром, меньше произведений действующих значений тока и напряжения: Р = cosj.
В цепи, не содержащей ни индуктивности, ни емкости, ток совпадает по фазе с напряжением (рис. 3). Закон Ома для действующих значений в этой цепи будет иметь такую же форму, как для цепи постоянного тока: = /r. Здесь r - активное сопротивление цепи, определяемое по активной мощности Р, затрачиваемой в цепи: r = /2.
При наличии в цепи индуктивности L П индуцирует в ней эдс самоиндукции eL = - L. di/dt = - wLlm cos (wt + a) = wLIm sin (wt + a - p/2). Эдс самоиндукции противодействует изменениям тока, и в цепи, содержащей только индуктивность, ток отстает по фазе от напряжения на четверть периода, то есть j=p/2 (рис. 4). Действующее значение eL равно EL = IwL = IxL, где xL = wL - индуктивное сопротивление цепи. Закон Ома для такой цепи имеет вид: = /xL = /wL.
Когда емкость С включена под напряжение u, то ее заряд равен q = . Периодические изменения напряжения вызывают периодические изменения заряда, и возникает емкостный ток i = dq/dt = ×du/dt = (m cos (wt + b) = wCUm sin (wt + b + p/2). Таким образом, синусоидальный П, проходящий через емкость, опережает по фазе напряжение на ее зажимах на четверть периода, то есть j = -p/2 (рис. 5). Эффективные значения в такой цепи связаны соотношением = w = /xc, где xc = 1/wС - емкостное сопротивление цепи.
Если цепь П состоит из последовательно соединенных r, L и С, то ее полное сопротивление равно 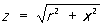 , где x = xL - xc = wL - 1/w - реактивное сопротивление цепи П Соответственно, закон Ома имеет вид: , где x = xL - xc = wL - 1/w - реактивное сопротивление цепи П Соответственно, закон Ома имеет вид: 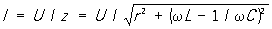 , а сдвиг фаз между током и напряжением определяется отношением реактивного сопротивления цепи к активному: tgj = х/r. В такой цепи при совпадении частоты w вынужденных колебаний, создаваемых источником П, с резонансной частотой w0 = 1/ , а сдвиг фаз между током и напряжением определяется отношением реактивного сопротивления цепи к активному: tgj = х/r. В такой цепи при совпадении частоты w вынужденных колебаний, создаваемых источником П, с резонансной частотой w0 = 1/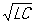 индуктивное и емкостное сопротивления равны (wL = 1/wС) и полностью компенсируют друг друга, сила тока максимальна и наблюдается явление резонанса (см. Колебательный контур). В условиях резонанса напряжения на индуктивности и емкости могут значительно (часто во много раз) превышать напряжение на зажимах цепи. индуктивное и емкостное сопротивления равны (wL = 1/wС) и полностью компенсируют друг друга, сила тока максимальна и наблюдается явление резонанса (см. Колебательный контур). В условиях резонанса напряжения на индуктивности и емкости могут значительно (часто во много раз) превышать напряжение на зажимах цепи.
Облегчение расчетов цепей синусоидальных П достигается построением так называемых векторных диаграмм. Векторы синусоидальных тока и напряжения принято помечать точкой над буквенным обозначением (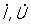 ). Длины векторов обычно берутся равными (в масштабе построения диаграммы) действующим значениям и , а углы между векторами - равными сдвигам фаз между мгновенными значениями соответствующих величин. Алгебраическому сложению мгновенных значений синусоидальных величин одной и той же частоты соответствует геометрическое сложение векторов этих величин. На рис. 6 показана векторная диаграмма для цепи П с последовательно соединенными r, L, С. Мгновенное значение напряжения на зажимах этой цепи равно алгебраической сумме напряжений на активном и реактивном сопротивлениях: u = uL + ur + uc, следовательно, ). Длины векторов обычно берутся равными (в масштабе построения диаграммы) действующим значениям и , а углы между векторами - равными сдвигам фаз между мгновенными значениями соответствующих величин. Алгебраическому сложению мгновенных значений синусоидальных величин одной и той же частоты соответствует геометрическое сложение векторов этих величин. На рис. 6 показана векторная диаграмма для цепи П с последовательно соединенными r, L, С. Мгновенное значение напряжения на зажимах этой цепи равно алгебраической сумме напряжений на активном и реактивном сопротивлениях: u = uL + ur + uc, следовательно, 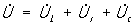 . При построении диаграммы исходным служит вектор тока, так как во всех участках неразветвленной цепи ток один и тот же. Поскольку индуктивное напряжение опережает по фазе ток на p/2, а емкостное отстает от тока на p/2 (то есть они находятся в противофазе), при последовательном соединении они друг друга частично компенсируют. . При построении диаграммы исходным служит вектор тока, так как во всех участках неразветвленной цепи ток один и тот же. Поскольку индуктивное напряжение опережает по фазе ток на p/2, а емкостное отстает от тока на p/2 (то есть они находятся в противофазе), при последовательном соединении они друг друга частично компенсируют.
Векторные диаграммы наглядно иллюстрируют ход вычислений и служат для контроля над ними; построенные с соблюдением масштаба, они позволяют графически определить эффективное напряжение в цепи и угол сдвига фаз j.
Для расчетов разветвленных цепей квазистационарного П используют Кирхгофа правила. При этом обычно применяют метод комплексных величин (символический метод), который позволяет выразить в алгебраической форме геометрические операции с векторами П и применить, таким образом, для расчетов цепей П все методы расчетов цепей постоянного тока.
Несинусоидальность П в электроэнергетических системах обычно нежелательна, и принимаются специальные меры для ее подавления. Но в цепях электросвязи, в полупроводниковых и электронных устройствах несинусоидальность создается самим рабочим процессом. Если среднее за период значение тока не равно нулю, то он содержит постоянную составляющую. Для анализа процессов в цепях несинусоидального тока его представляют в виде суммы простых гармонических составляющих, частоты которых равны целым кратным числам основной частоты: = i0 + 1m sin (wt + a1)+ 2m sin (2wt + a2) +... + lkm sin (kwt + ak). Здесь 0 - постоянная составляющая тока, imsin (wt + a1) - первая гармоническая составляющая (основная гармоника), остальные члены - высшие гармоники. Расчет линейных цепей несинусоидального тока на основании принципа суперпозиции (наложения) ведется для каждой составляющей (так как xL и xc зависят от частоты). Алгебраическое сложение результатов таких расчетов дает мгновенное значение силы (или напряжения) несинусондального тока.
Лит.: Теоретические основы электротехники, 3 изд., ч. 2, М., 1970; Нейман Л. Р., Демирчан К. С., Теоретические основы электротехники, т. 1-2, М.- Л., 1966; Касаткин А. С., Электротехника, 3 изд., М., 1974; Поливанов К. М., Линейные электрические цепи с сосредоточенными постоянными, М., 1972 (Теоретические основы электротехники, т. 1).
А. С. Касаткин.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|