|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Парсеваля равенство | Парсеваля равенство (далее П) равенство вида
 ,
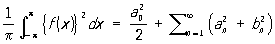где a0, an, bn— коэффициенты Фурье функции f (x). Установлено в 1805 французским математиком М. Парсевалем (М. Parseval) при предположении о возможности почленного интегрирования тригонометрических рядов. В 1896 А. М. Ляпунов доказал, что это равенство справедливо, если функция ограничена в интервале (—p,p) и существует интеграл 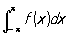 . Позже было установлено, что П справедливо для любых функций с интегрируемым квадратом. В работах В. А. Стеклова установлена справедливость П для рядов по др. ортогональным системам функций. См. также Тригонометрический ряд, Ортогональная система функций. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 21.11.2024 12:13:28
|
|
|
|
|
|
|
|
|
|
|
