
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Остроградского формула | Остроградского формула (далее О) формула, дающая преобразование интеграла, взятого по объему Q, ограниченному поверхностью , в интеграл, взятый по этой поверхности:
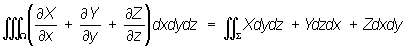 ; ;
здесь X, , Z — функции точки (х, у, z), принадлежащей трехмерной области . О найдена М. В. Остроградским в 1828 (опубликована в 1831). В векторной форме О имеет вид:
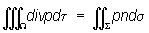 , ,
где р — вектор поля, заданного в области ; dt — элемент объема; n — единичный вектор внешней нормали к поверхности ; ds — элемент этой поверхности. В гидродинамическом истолковании О устанавливает равносильность двух способов учета того количества жидкости, которое вытекает из оболочки в единицу времени: 1) исходя из "производительности" точечных источников, заполняющих область (левая часть равенства); 2) исходя из скоростей частиц жидкости в момент их прохождения через оболочку (правая часть равенства). Формула была дана Остроградским (1834, опубликована в 1838) также и в более общем виде — для интеграла, распространенного на n-мерную область. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|