
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Остаточный член | Остаточный член (далее О) приближенной формулы, разность между точным и приближенным значениями представляемого этой формулой выражения. В зависимости от характера приближенной формулы О может иметь различный вид. Обычно задача исследования О состоит в том, чтобы получить для него оценки. Например, приближенной формуле
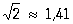
соответствует точное равенство
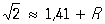 , ,
где выражение R является О для приближения 1,41 к числу 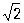 и известно, что 0,004 < R < 0,005. Далее, О постоянно встречается в асимптотических формулах. Например, для числа p(х) простых чисел, не превосходящих х, имеем асимптотическую формулу и известно, что 0,004 < R < 0,005. Далее, О постоянно встречается в асимптотических формулах. Например, для числа p(х) простых чисел, не превосходящих х, имеем асимптотическую формулу
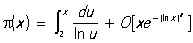 , ,
где m - любое положительное число, меньшее 3/5; здесь О, являющийся разностью
между функциями p(х) и 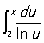 для х ³ 2, записан в виде для х ³ 2, записан в виде 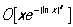 , где буква О обозначает, что О не превосходит по абсолютной величине выражения , где буква О обозначает, что О не превосходит по абсолютной величине выражения 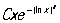 , а С - некоторая положительная постоянная. Можно говорить об О формулы, дающей приближенное представление функции. Например, в Тейлора формуле , а С - некоторая положительная постоянная. Можно говорить об О формулы, дающей приближенное представление функции. Например, в Тейлора формуле
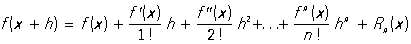
О Rn (x) в форме Лагранжа имеет вид
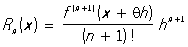 , ,
где q - некоторое число, причем 0 < q < 1 (q зависит, вообще говоря, от выбранных значений х и h). Наличие в формуле для Rn (x) числа q вносит некоторую неопределенность; такого рода неопределенность свойственна многим формулам для О
Можно говорить об О квадратурной формулы, интерполяционных формул и т.д. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 12:29:01
|

|

|
 |
|

|
 |
 |
 |
|