
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Операционное исчисление | Операционное исчисление (далее О), один из методов математического анализа, позволяющий в ряде случаев посредством простых правил решать сложные математические задачи. О имеет особенно важное значение в механике, автоматике, электротехнике и др. В основе метода О лежит идея замены изучаемых функций (оригиналов) некоторыми др. функциями (изображениями), получаемыми из первых по определенным правилам (обычно, изображение — функция, получаемая из данной Лапласа преобразованием). При такой замене оператор дифференцирования р = 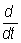 интерпретируется как алгебраическая величина, вследствие чего интегрирование некоторых классов линейных дифференциальных уравнений и решение ряда др. задач математического анализа сводится к решению более простых алгебраических задач. Так, решение линейного дифференциального уравнения сводится к более простой, вообще говоря, задаче решения алгебраического уравнения; из алгебраического уравнения находят изображение решения данного уравнения, после чего по изображению восстанавливают само решение. Операции нахождения изображения по оригиналу (и наоборот) облегчаются наличием обширных таблиц "оригинал — изображение". интерпретируется как алгебраическая величина, вследствие чего интегрирование некоторых классов линейных дифференциальных уравнений и решение ряда др. задач математического анализа сводится к решению более простых алгебраических задач. Так, решение линейного дифференциального уравнения сводится к более простой, вообще говоря, задаче решения алгебраического уравнения; из алгебраического уравнения находят изображение решения данного уравнения, после чего по изображению восстанавливают само решение. Операции нахождения изображения по оригиналу (и наоборот) облегчаются наличием обширных таблиц "оригинал — изображение".
Для развития О большое значение имели работы английского ученого О. Хевисайда. Он предложил формальные правила обращения с оператором р = 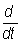 и некоторыми функциями от этого оператора. Пользуясь О, Хевисайд решил ряд важнейших задач электродинамики. Однако О не получило в трудах Хевисайда математического обоснования, многие его результаты оставались недоказанными. Строгое обоснование О было дано с помощью интегрального преобразования Лапласа. Если при этом преобразовании функция f (t), 0 £ t < + ¥, переходит в функцию (z), z = x+iy: и некоторыми функциями от этого оператора. Пользуясь О, Хевисайд решил ряд важнейших задач электродинамики. Однако О не получило в трудах Хевисайда математического обоснования, многие его результаты оставались недоказанными. Строгое обоснование О было дано с помощью интегрального преобразования Лапласа. Если при этом преобразовании функция f (t), 0 £ t < + ¥, переходит в функцию (z), z = x+iy:
f (t) ® (z),
то производная
f (t) ® zF (z) – f (0) (*)
и интеграл
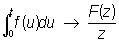 . .
Следовательно, оператор дифференцирования р переходит в оператор умножения на переменную z, а интегрирование сводится к делению на z. В след. краткой таблице даны (при t ³ 0) примеры соответствия
оригинал ®
|
изображение
|
f (t)
|
(z)
|
1
|
1/z
|
t n
|
n!/z n+1 (n > 0 – целое)
|
е lt
|
1/(z – l)
|
cos wt
|
z/(z 2 + w2)
|
sin wt
|
w/(z 2 + w2)
|
Пример. Найти методом О решение у = f (t) линейного дифференциального уравнения
у” – у" – 6у = 2e 4t
при начальных условиях
y0 = f (0) = 0 и y0"=f`(0) = 0.
Переходя от искомой функции f (t) и данной функции 2e4t к их изображениям (z) и 2/(z – 4) (см. табл.) и применяя формулу (*) для изображения производных, получим
z2 (z) – zF (z) – 6 (z) = 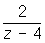 , ,
или
(z) = 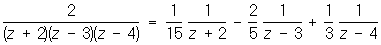 . .
Откуда (опять по таблице)
y = f (t) = 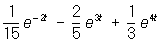
Другой путь обоснования О предложен польским математиком Я. Микусиньским (1953), опиравшимся на понятие функционального кольца. Для обоснования методов О можно воспользоваться теорией обобщенных функций. Имеются различные обобщения О Существует многомерное О, основанное на теории кратных интегралов. Созданы О дифференциальных операторов, отличных от оператора р = 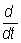 , например = , например = 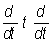 . Эти теории также основываются на изучении функциональных колец, в которых надлежащим образом определено понятие произведения функций. . Эти теории также основываются на изучении функциональных колец, в которых надлежащим образом определено понятие произведения функций.
Лит.: Диткин В. А., Прудников А. П., Справочник по операционному исчислению, М., 1965; их же, О, М., 1966; Микусинский Я., О, пер. с польск., М., 1956; Штокало И. 3., О, К., 1972.
В. А. Диткин. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 13:18:45
|

|

|
 |
|

|
 |
 |
 |
|