
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Операторов теория | Операторов теория (далее О), часть функционального анализа, посвященная изучению свойств операторов и применению их к решению различных задач. Понятие оператора — одно из самых общих математических понятий.
Примеры:
1) Отнеся каждому вектору (x1, x2, x3) вектор (x`1, x"2, x`3) так, что x`i = ai1x1 + ai2x2 + ai3x3 (i = 1, 2, 3; ai1, ai2, ai3 — фиксированные числа), получим некоторый оператор.
2) Операция (оператор) дифференцирования D (f (t)) = f`(t) относит каждой дифференцируемой функции f (t) ее производную f` (t).
3) Операция (оператор) определенного интегрирования =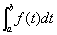 относит каждой интегрируемой функции действительное число. относит каждой интегрируемой функции действительное число.
4) Отнеся каждой функции f (t) ее произведение j(t) f (t) на фиксированную функцию j(t), снова получаем оператор.
Общая О возникла в результате развития теории интегральных уравнений, решения задач на нахождение собственных функций и собственных значений для дифференциальных операторов (см., например, Штурма — Лиувилля задача) и др. разделов классического анализа. О установила тесные связи между этими разделами математики и сыграла важную роль в их дальнейшем развитии. Еще до возникновения общего понятия оператора операторные методы широко применялись в решении различных типов дифференциальных уравнений, обыкновенных и с частными производными (см. Операционное исчисление). О представляет собой основной математический аппарат квантовой механики (см. Операторы в квантовой теории).
Операторы в линейных пространствах. Чаще всего встречаются операторы, действующие в линейных нормированных пространствах (см. Линейное пространство), в частности в функциональных пространствах, т. е. отображения у = А (х) линейного пространства R или его части в некоторое линейное пространство R" (возможно, совпадающее с R). Этот класс операторов охватывает такие важнейшие понятия, как числовые функции, линейные преобразования евклидова пространства, дифференциальные и интегральные операторы (см. ниже) и т.д. Наиболее изученными и важными для приложений являются линейные операторы. Оператор называется линейным, если A (ax+by) = aА (х) + bА (у) для любых элементов х, у пространства R и любых чисел a, b. Если пространства R и R" нормированы, а отношение 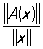 нормы А (х) к норме х ограничено, то линейный оператор A называется ограниченным, а верхнюю грань отношения нормы А (х) к норме х ограничено, то линейный оператор A называется ограниченным, а верхнюю грань отношения 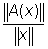 его нормой. Ограниченность линейного оператора равносильна его непрерывности, т. е. тому, что А (Хп) ® А (х), когда Хп ® х. Оператор дифференцирования (пример 2) представляет собой один из важнейших примеров неограниченного (а следовательно, и не непрерывного) линейного оператора. См. также Линейный оператор. его нормой. Ограниченность линейного оператора равносильна его непрерывности, т. е. тому, что А (Хп) ® А (х), когда Хп ® х. Оператор дифференцирования (пример 2) представляет собой один из важнейших примеров неограниченного (а следовательно, и не непрерывного) линейного оператора. См. также Линейный оператор.
Приведенные выше примеры 1—4 представляют собой примеры линейных операторов. Дальнейшие примеры линейных операторов:
5) Пусть k (s, t ) — непрерывная функция двух переменных, заданная в квадрате a £ s £ b, а £ t £ b. Формула
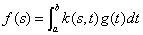
определяет линейный интегральный оператор, называется оператором Фредгольма.
6) Каждой абсолютно интегрируемой на всей прямой функции f (t) поставим в соответствие функцию
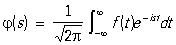
называется Фурье преобразованием исходной функции. Это соответствие также представляет собой линейный оператор.
7) Левую часть линейного дифференциального уравнения
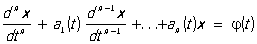
можно рассматривать как результат применения некоторого оператора, ставящего в соответствие функции x (t) функцию j(t). Такой оператор носит название линейного дифференциального оператора. Простейшим частным случаем линейного дифференциального оператора является оператор дифференцирования.
Примеры нелинейных операторов:
8) Пусть A(f (t)) = f 2(t); определенный т. о. оператор является нелинейным.
9) Пусть
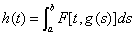
( — некоторая ограниченная непрерывная функция). Соответствие g ® h, определяемое этой формулой, представляет собой нелинейный интегральный оператор.
Действия над операторами. Пусть дан оператор
у = А (х),
причем никакие два разных элемента х и х" не переходят в один и тот же элемент у. Тогда каждому образу у отвечает его единств. прообраз х. Это соответствие называется обратным оператором и обозначают
х = А–1(у).
Построение обратного оператора эквивалентно решению уравнения у = А (х) относительно х (отыскание неизвестного прообраза по данному образу).
Если A1 и А2 — два оператора, отображающих R в R", то их суммой А = A1 + A2 называется оператор, определяемый равенством А (х) = A1(x) + A2(x). Если оператор A1 переводит R в R", а A2 переводит R" в R”, то результат их последовательного применения представляет собой оператор, отображающий R в R”; его называют произведением A2A1 операторов A1 и A2. Если, в частности, рассматриваются операторы, переводящие некоторое линейное пространство в себя, то сумма и произведение двух таких операторов всегда определены. Результат последовательного применения п раз одного и того же оператора А есть n-я степень An этого оператора. Например, n-я степень оператора дифференцирования есть оператор n-kpaтного дифференцирования Dn (f (t)) = f (n)(t). Произведение lА оператора А на число l определяется формулой
(lА)(х) = lА (х).
Оператор Е, переводящий всякий элемент х в самого себя, называется единичным. Нулевым называется оператор О, переводящий каждый элемент в нуль. Очевидно, что при любом А справедливы равенства: AE = EA = А и А+О = О + А = А, далее, если, А–1 существует, то А–1А = AA–1 = Е (следует заметить, что для двух произвольных операторов А и В произведения AB и BA, вообще говоря, не равны между собой).
С помощью операций сложения, умножения операторов и умножения операторов на числа можно определить многочлены от линейного оператора, а путем предельного перехода, понимаемого соответствующим образом, — и более сложные функции от оператора. Например, если D — оператор дифференцирования, то eD означает оператор, определяемый формулой
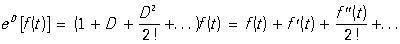 , ,
имеющий смысл для тех f (t), для которых ряд справа сходится. Для аналитических функций сумма этого ряда равна f (t + 1), т. е. eD — оператор сдвига, переводящий f (t) в f (t + 1).
Линейные операторы в гильбертовом пространстве. Наиболее полно О разработана для случая линейных операторов в гильбертовом пространстве. Пусть А — ограниченный линейный оператор в гильбертовом пространстве . Комплексное число l называется собственным значением оператора А, если существует такой элемент х ¹ 0 из , что А (х) = lх; при этом х называется собственным вектором оператора А, отвечающим данному собственному значению. Число l называется регулярной точкой оператора А, если оператор (А + lЕ)–1 существует, определен на всем Н и ограничен; остальные значения l называется точками спектра оператора А. Каждое собственное значение принадлежит спектру, их совокупность образует точечный спектр, остальную часть спектра называется непрерывным спектром. Тот факт, что спектр линейного оператора, вообще говоря, не исчерпывается его собственными значениями, представляет собой характерную черту линейных операторов в бесконечномерном пространстве, отличающую их от линейных преобразований конечномерного евклидова пространства.
Оператор А* называется сопряженным к А, если скалярное произведение (Ax, у) = (х, А*у) для всех х и у из Н. Оператор А называется самосопряженным, если А = А*, и унитарным, если А* = А–1. Самосопряженные и унитарные операторы представляют собой важнейшие и наиболее полно изученные классы линейных операторов в гильбертовом пространстве. Их теория является обобщением теории самосопряженных и унитарных линейных преобразований n-мерного евклидова пространства. См. также Спектральный анализ (математический).
Одним из простейших классов ограниченных линейных операторов в гильбертовом пространстве являются вполне непрерывные операторы. Оператор А называется вполне непрерывным, если он переводит всякое ограниченное множество из Н в компактное (см. Компактность). Спектр вполне непрерывного оператора состоит из конечного или бесконечного счетного числа собственных значений и не имеет отличных от нуля предельных точек. Каждому l ¹ 0 отвечает лишь конечное число линейно независимых собственных функций. Непрерывный спектр отсутствует.
Самосопряженный вполне непрерывный оператор А имеет хотя бы одно собственное значение, причем в Н можно выбрать полную ортогональную систему элементов, состоящую из собственных функций оператора А.
Неограниченные операторы. Понятие ограниченного линейного оператора оказывается во многих случаях слишком узким. Поэтому возникла необходимость рассматривать т. н. неограниченные операторы. Соответствующее, более общее, определение гласит: оператор А называется линейным неограниченным оператором в гильбертовом пространстве Н, если: 1) соответствие у = А (х) определено для всех х, принадлежащих некоторому линейному многообразию , называемому областью определения оператора A; 2) А (aх + by) = aА (х) + bA (y).
Важнейшим классом неограниченных линейных операторов в гильбертовом пространстве являются дифференциальные операторы. Многие задачи математической физики, в частности теории колебаний, приводят к задаче о разыскании собственных функций и собственных значений различных дифференциальных операторов. Например, цилиндрические функции, Лежандра многочлены и т.д. представляют собой не что иное, как собственные функции определенных дифференциальных операторов.
Нелинейные операторы. При изучении операторов предположение об их линейности играет весьма существенную роль. Однако в ряде случаев приходится рассматривать и нелинейные операторы. В частности, важное значение в механике и физике имеют нелинейные интегральные уравнения.
Лит.: Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 3 изд., М., 1972; Данфорд Н., Шварц Дж. Т., Линейные операторы. Общая теория, пер. с англ., М., 1962. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|