
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Обратная матрица | Обратная матрица (далее О) для данной квадратной матрицы А = 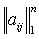 порядка n такая матрица В = порядка n такая матрица В = 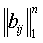 (того же порядка), что АВ = Е, где Е — единичная матрица; тогда выполняется также и равенство ВА = Е. О обозначается через А-1. Для существования О А-1 необходимо и достаточно, чтобы определитель данной матрицы А был отличен от нуля, т. е. чтобы матрица А была неособенной; элементы bij О находятся по формуле bij = Ajii/D, где Ajii — алгебраическое дополнение элемента aij матрицы A, a D — определитель матрицы А. (того же порядка), что АВ = Е, где Е — единичная матрица; тогда выполняется также и равенство ВА = Е. О обозначается через А-1. Для существования О А-1 необходимо и достаточно, чтобы определитель данной матрицы А был отличен от нуля, т. е. чтобы матрица А была неособенной; элементы bij О находятся по формуле bij = Ajii/D, где Ajii — алгебраическое дополнение элемента aij матрицы A, a D — определитель матрицы А.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|