
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Обменное взаимодействие | Обменное взаимодействие (далее О), специфическое взаимное влияние одинаковых, тождественных, частиц, эффективно проявляющееся как результат некоторого особого взаимодействия. О — чисто квантовомеханический эффект, не имеющий аналога в классической физике (см. Квантовая механика). Вследствие квантовомеханического принципа неразличимости одинаковых частиц (тождественности принципа) волновая функция системы должна обладать определенной симметрией относительно перестановки двух одинаковых частиц, т. е. их координат и спинов: для частиц с целым спином — бозонов — волновая функция системы не меняется при такой перестановке (является симметричной), а для частиц с полуцелым спином — фермионов — меняет знак (является антисимметричной). Если силы взаимодействия между частицами не зависят от их спинов, волновую функцию системы можно представить в виде произведения двух функций, одна из которых зависит только от координат частиц, а другая — только от их спинов. В этом случае из принципа тождественности следует, что координатная часть волновой функции, описывающая движение частиц в пространстве, должна обладать определенной симметрией относительно перестановки координат одинаковых частиц, зависящей от симметрии спиновой функции. Наличие такой симметрии означает, что имеет место определенная согласованность, корреляция, движения одинаковых частиц, которая сказывается на энергии системы (даже в отсутствие каких-либо силовых взаимодействий между частицами). Поскольку обычно влияние частиц друг на друга является результатом действия между ними каких-либо сил, о взаимном влиянии одинаковых частиц, вытекающем из принципа тождественности, говорят как о проявлении специфического взаимодействия — О Возникновение О можно проиллюстрировать на примере (впервые это было сделано В. Гейзенбергом в 1926). Спиновые взаимодействия в легких малы, поэтому волновая функция двух электронов в может быть представлена в виде:
= Ф (r1, r2)c(s1, s2), (1)
где Ф (r1, r2) — функция от координат r1, r2 электронов, а c(s1, s2) — от проекции их спинов s1, s2 на некоторое направление. Т. к. электроны являются полная волновая функция y должна быть антисимметричной. Если суммарный спин 5 обоих электронов равен нулю (спины антипараллельны — парагелий), то спиновая функция c антисимметрична относительно перестановки спиновых переменных и, следовательно, координатная функция Ф должна быть симметрична относительно перестановки координат электронов. Если же полный спин системы равен 1 (спины параллельны — ортогелий), то спиновая функция симметрична, а координатная — антисимметрична. Обозначая через yп (r1), yп" (r2) волновые функции отдельных электронов в (индексы n, n" означают набор квантовых чисел, определяющих состояние электрона в можно, пренебрегая сначала взаимодействием между электронами, записать координатную часть волновой функции в виде:
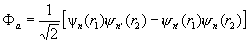
для случая = 1, (2)
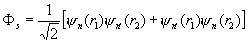
для случая = 0 (2")
(множитель 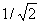 введен для нормировки волновой функции). В состоянии с антисимметричной координатной функцией Фа ср. расстояние между электронами оказывается большим, чем в состоянии с симметричной функцией Ф; это видно из того, что вероятность ||2 = |Фа|2 |c|2 нахождения электронов в одной и той же точке r1 = r2 для состояния Фа равна нулю. Поэтому средняя энергия кулоновского взаимодействия (отталкивания) двух электронов оказывается в состоянии Фа меньшей, чем в состоянии Ф. Поправка к энергии системы, связанная с взаимодействием электронов, определяется по теории возмущении и равна: введен для нормировки волновой функции). В состоянии с антисимметричной координатной функцией Фа ср. расстояние между электронами оказывается большим, чем в состоянии с симметричной функцией Ф; это видно из того, что вероятность ||2 = |Фа|2 |c|2 нахождения электронов в одной и той же точке r1 = r2 для состояния Фа равна нулю. Поэтому средняя энергия кулоновского взаимодействия (отталкивания) двух электронов оказывается в состоянии Фа меньшей, чем в состоянии Ф. Поправка к энергии системы, связанная с взаимодействием электронов, определяется по теории возмущении и равна:
ЕВ3 = К ± А, (3)
где знаки ± относятся соответственно к симметричному Ф и антисимметричному Фа координатным состояниям,
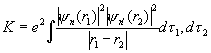 (4) (4)
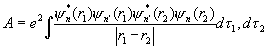
(dt = dxdydz — элемент объема). Величина К имеет вполне наглядный классический смысл и соответствует электростатическому взаимодействию двух заряженных "облаков" с плотностями заряда еçyn (r1)ç2 и еçyn¢(r2)ç2. Величину А, называется обменным интегралом, можно интерпретировать как электростатическое взаимодействие заряженных "облаков" с плотностями заряда еyn*(r1)yn¢(r1) и еyn¢*(r1)yn¢(r2) yn (r2), т. е. когда каждый из электронов находится одновременно в состояниях yn и yn¢ (что бессмысленно с точки зрения классической физики). Из (3) следует, что полная энергия пара- и ортогелия с электронами в аналогичных состояниях отличается на величину 2А. Т. о., хотя непосредственно спиновое взаимодействие мало и не учитывается, тождественность двух электронов в приводит к тому, что энергия системы оказывается зависящей от полного спина системы, как если бы между частицами существовало дополнительное, обменное, взаимодействие. Очевидно, что О в данном случае является частью кулоновского взаимодействия электронов и явным образом выступает при приближенном рассмотрении квантовомеханической системы, когда волновая функция всей системы выражается через волновые функции отдельных частиц (в частности, в приближении Хартри — Фока; см. Самосогласованное поле).
О эффективно проявляется, когда "перекрываются" волновые функции отдельных частиц системы, т. е. когда существуют области пространства, в которых с заметной вероятностью может находиться частица в различных состояниях движения. Это видно из выражения для обменного интеграла А: если степень перекрытия состояний yn*(r) и yn¢(r) незначительна, то величина А очень мала.
Из принципа тождественности следует, что О возникает в системе одинаковых частиц даже в случае, если прямыми силовыми взаимодействиями частиц можно пренебречь, т. е. в идеальном газе тождественных частиц. Эффективно оно начинает проявляться, когда среднее расстояние между частицами становится сравнимым (или меньшим) длины волны де Бройля, соответствующей средней скорости частиц. При этом характер О различен для и для бозонов. Для О является следствием Паули принципа, препятствующего сближению тождественных частиц с одинаковым направлением спинов, и эффективно проявляется как отталкивание их друг от друга на расстояниях порядка или меньше длины волны де Бройля; отличие от нуля энергии вырожденного газа ( целиком обусловлено таким О В системе тождественных бозонов О, напротив, имеет характер взаимного притяжения частиц. В этих случаях рассмотрение систем, состоящих из большого числа одинаковых частиц, производится на основе квантовой статистики (Ферми — Дирака статистики для и Бозе — Эйнштейна статистики для бозонов).
Если взаимодействующие тождественные частицы находятся во внешнем поле, например в кулоновском поле ядра, то существование определенной симметрии волновой функции и соответственно определенной корреляции движения частиц влияет на их энергию в этом поле, что также является семенным эффектом. Обычно (в молекуле, это О вносит вклад обратного знака по сравнению с вкладом О частиц друг с другом. Поэтому суммарный обменный эффект может как понижать, так и повышать полную энергию взаимодействия в системе. Энергетическая выгодность или невыгодность состояния с параллельными спинами в частности электронов, зависит от относительных величин этих вкладов. Так, в ферромагнетике (аналогично рассмотренному более низкой энергией обладает состояние, в котором спины электронов в незаполненных оболочках соседних параллельны; в этом случае благодаря О возникает спонтанная намагниченность (см. Ферромагнетизм). Напротив, в молекулах с ковалентной химической связью, например в молекуле Н2, энергетически выгодно состояние, в котором спины валентных электронов соединяющихся антипараллельны.
О объясняет, т. о., закономерности и молекулярной спектроскопии, связь в молекулах, ферромагнетизм (и антиферромагнетизм), а также др. специфические явления в системах одинаковых частиц.
Термином "О" обозначают также силы взаимодействия, не обусловленные тождественностью частиц, но приводящие к "обмену" между частицами некоторыми их характеристиками. Так, среди различных типов ядерных сил имеются силы, благодаря которым нуклоны (протоны и нейтроны) ядра "обмениваются" координатами, направлениями спинов, электрическими зарядами (т. н. обменные силы). Такие силы возникают вследствие того, что нуклоны могут обмениваться различного типа мезонами, переносящими заряд, спин и др. квантовые характеристики от одного нуклона к другому. Подробнее см. Ядерные силы.
Лит.: Блохинцев Д. И., Основы квантовой механики, 3 изд., М., 1961; Гамбош П., Статистическая теория и ее применения, пер. с нем., М., 1951; Вонсовский С. В., Шур Я. С., Ферромагнетизм, М. — Л., 1948; Давыдов А. С., Теория ядра, М., 1958.
Д. А. Киржниц, С. С. Герштейн. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |
|