
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Ньютона метод | Ньютона метод (далее Н), метод приближенного нахождения корня x0 уравнения f (x) = 0, называемый также методом касательных. Н состоит в том, что по исходному ("первому") приближению х = a1 находят второе (более точное), проводя касательную к графику (см. рис.) у = f (x) в точке А (а1 f (a1)) до ее пересечения с осью Ox; точка пересечения х = a1 - f (a1)/f`(a1) и принимается за новое значение a2. корня. Повторяя в случае необходимости этот процесс, получают все более и более точные приближения a2, a3,... корня x0 при условии, что производная f`(x) монотонна и сохраняет знак на сегменте, содержащем x0. Ошибка e2 = x0 -a2 нового значения a2 связана со старой ошибкой e1 = x0 - a1 формулой 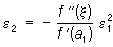 , где , где 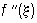 - значение второй производной функции f (x) в некоторой точке x, лежащей между x0 и a1. Иногда рекомендуется Н применять одновременно с к.-л. другим способом, например с линейного интерполирования методом. Н допускает обобщения, которые позволяют применять его для решения уравнений (x) = 0 в нормированных пространствах (- оператор в этом пространстве), в частности для решения систем уравнений и функциональных уравнений. Метод разработан И. Ньютоном в 1669. - значение второй производной функции f (x) в некоторой точке x, лежащей между x0 и a1. Иногда рекомендуется Н применять одновременно с к.-л. другим способом, например с линейного интерполирования методом. Н допускает обобщения, которые позволяют применять его для решения уравнений (x) = 0 в нормированных пространствах (- оператор в этом пространстве), в частности для решения систем уравнений и функциональных уравнений. Метод разработан И. Ньютоном в 1669.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 27.07.2024 03:47:53
|

|

|
 |
|

|
 |
 |
 |
|