|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Нормированное кольцо | Нормированное кольцо (далее Н), важное понятие функционального анализа, значительно расширившее область его приложений. Элементы Н являются одновременно и точками некоторого геометрического образования - полного нормированного пространства, и элементами некоторого алгебраического образования - кольца, в котором определено еще умножение на числа (причем алгебраические операции непрерывны по норме). Примерами Н могут служить: кольцо С всех непрерывных функций на отрезке (0,1) с обычными алгебраическими операциями и нормой 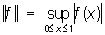 , кольцо L1 всех абсолютно интегрируемых на прямой функций, в котором умножение определено как свертывание:
 ,  ;
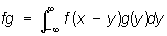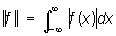кольцо матриц n-го порядка; кольцо ограниченных операторов гильбертова пространства - кольцо операторов, и т.д. Наиболее разработана теория коммутативных Н (т. е. Н, в которых умножение перестановочно: ху = ух), созданная И. М. Гельфандом.
Наряду с термином "Н" употребляется термин "банахова алгебра".
Лит.: Наймарк М. А., Нормированные кольца, М., 1956.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 21.11.2024 12:02:34
|
|
|
|
|
|
|
|
|
|
|
