|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Нормальный алгорифм | Нормальный алгорифм (далее Н), одно из современных уточнений понятия алгоритма, получившее распространение в исследованиях по конструктивной математике. Предложено в 1950 А. А. Марковым, впервые систематически и строго построившим на основе этого уточнения общую алгоритмов теорию. Н эквивалентны частично-рекурсивным функциям (см. Рекурсивные функции), а следовательно, и Тьюринга машинам.
Концепция Н специально приспособлена для реализации алгоритмов, действующих над словами в тех или иных алфавитах. При этом под алфавитом в математике понимается любой конечный набор четко отличимых друг от друга графических символов (букв), а под словом в данном алфавите - произвольная конечная цепочка букв этого алфавита. Цепочка, вовсе не содержащая букв, также считается словом в данном алфавите (пустое слово). Например, цепочки "ииаам", "книга", "гамма" являются словами в русском алфавите, а также в шестибуквенном алфавите {к, н, и, г, а, м}. Элементарным актом преобразования слов в алгоритмических процессах, задаваемых Н, является т. н. операция "подстановки вместо первого вхождения". Пусть Р, Q, R - слова в некотором алфавите. Результатом подстановки Q вместо первого вхождения Р в R называется слово å (R, Р, Q), получаемое следующим образом. Если Р входит в R, т.е. R представимо в виде 12, то среди таких представлений отыскивается представление с наиболее коротким словом 1 и полагается å (R, Р, Q) = 1QS2. Если же Р не входит в R, то å (R, Р, Q) = R. Так, å (гамма, а, е) = гемма.
Для задания Н 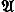 необходимо фиксировать некоторый алфавит А, не содержащий букв "®" и " · ", и упорядоченный список слов вида Р ® Q (простая формула подстановки) или Р ® · Q (заключит. формула подстановки), где Р и Q - слова в А. Формулы подстановок принято записывать друг под другом в порядке следования, объединяя их слева фигурной скобкой. Получающаяся фигура называется схемой Н Исходными данными и результатами работы Н 
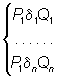
где di (1 £ i £ n) означает "®" или "®", разворачивается следующим образом. Отыскивается наименьшее i, при котором i входит в R. Если все i не входят в R, то работа  можно построить Н  , являющийся композицией и , т. е. реализующий следующий интуитивный алгоритм: "сначала выполнить алгоритм , затем к результату применять ".
Соотношение между интуитивными алгоритмами и Н описывается выдвинутым А. А. Марковым принципом нормализации: всякий алгоритм, перерабатывающий слова в данном алфавите А в слова в этом же алфавите, может быть реализован посредством Н в некотором расширении А. (Легко указать очень простые алгоритмы в А, не реализуемые Н в A; с другой стороны, всегда можно ограничиться двухбуквенным (и даже однобуквенным) расширением A.) Принцип нормализации эквивалентен тезису Черча и, аналогично последнему, не может быть доказан из-за неточности интуитивной концепции алгоритма.
Лит.: Марков А. А., Теория алгорифмов, М. - Л., 1954 (Тр. Математического института АН СССР, т. 42); Мендельсон Э., Введение в математическую логику, пер. с англ., М., 1971.
Б. А. Кушнер.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 21.11.2024 12:10:39
|
|
|
|
|
|
|
|
|
|
|
