
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Нормальное сечение | Нормальное сечение (далее Н) поверхности в данной ее точке М — линия пересечения с плоскостью, проведенной через нормаль в точке М. С помощью Н изучается искривление поверхности в различных (касательных) направлениях, выходящих из точки М. Среди этих направлений имеются два (взаимно перпендикулярных) т. н. главных направления, для которых нормальная кривизна (т. е. кривизна соответствующего Н) достигает наибольшего и наименьшего значений k1 и k2 (т.н. главные кривизны в данной точке); при этом кривизны Н берутся со знаком + (или —), если направление вогнутости (см. Выпуклость и вогнутость) сечения совпадает (противоположно) с положительным направлением нормали к поверхности. Нормальные кривизны поверхности в произвольных направлениях весьма просто выражаются через главные кривизны. Именно, кривизна kn Н, проведенного в направлении, составляющем угол j с первым из указанных выше главных направлений, связана с k1 и k2 соотношением (формула Эйлера):
kn = k1 cos2 j + k2 sin2 j.
С помощью кривизн Н изучаются также кривизны наклонных сечений поверхности. Именно, кривизна k наклонного сечения плоскостью a, проходящей через данную касательную прямую а, выражается формулой Менье:
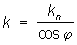
где j — угол между плоскостью a и нормалью к поверхности, kn — нормальная кривизна поверхности в направлении прямой а. См. также Дифференциальная геометрия, Поверхностей теория, Кривизна.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 13:23:19
|

|

|
 |
|

|
 |
 |
 |
|