
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Неприводимый многочлен | Неприводимый многочлен (далее Н), многочлен, не разлагающийся на множители более низкой степени. Возможность разложить многочлен на множители (и свойство неприводимости) зависит от того, какие числа допускаются в качестве коэффициентов многочлена. Так, многочлен x3 + 2 неприводим, если в качестве коэффициентов допускать только рациональные числа, но разлагается в произведение двух Н
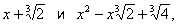
если в качестве коэффициентов брать любые действительные числа, и в произведение трех множителей
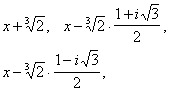
если коэффициентами будут числа комплексные. В общем случае понятие неприводимости определяется для многочленов с коэффициентами, принадлежащими произвольному полю (см. Поле алгебраическое). Часто Н называют многочлен с рациональными коэффициентами, не разлагающийся на множители более низкой степени также с рациональными коэффициентами.
Лит.: Курош А. Г., Курс высшей алгебры, 9 изд., М., 1968. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 27.07.2024 03:58:12
|

|

|
 |
|

|
 |
 |
 |
|