
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Непрерывная группа | Непрерывная группа (далее Н) математическое понятие, как и понятие обыкновенной группы, возникающее при рассмотрении преобразований. Пусть М - множество элементов х какого-либо рода, например чисел, точек пространства, функций и т.п. Говорят, что имеется преобразование f множества М, если каждому элементу x из М поставлен в соответствие определенный элемент
y = f (x), (1)
также принадлежащий М; при этом предполагается, что для каждого у найдется такой элемент х, и притом единственный, который удовлетворяет уравнению (1). Т. о., уравнение (1) разрешимо относительно х:
x = f--1(y),
и f--1 также есть преобразование множества М. Преобразование f-1 называется обратным к преобразованию f. Преобразование е, переводящее каждый элемент х в себя, е (х) = х, называется тождественным. Если имеется два преобразования f и g, то последовательное их применение дает новое преобразование k:
k (x) = f (g (x)).
Преобразование k называется произведением преобразований f и g:
k = fg.
Умножение некоторого преобразования f на тождественное е не меняет его:
fe = ef = f. (2)
Произведение преобразования f на его обратное f--1 дает тождественное:
ff-1 = f-1f = e. (3)
Для любых трех преобразований имеет место ассоциативный закон:
(fg) h = f (gh). (4)
Совокупность всех преобразований множества М является группой. Можно, однако, рассматривать совокупность не всех преобразований, а любую такую совокупность преобразований, что наряду с каждым преобразованием в нее входит обратное к нему, а наряду с каждыми двумя - их произведение. Тогда мы также имеем группу преобразований (подгруппу группы всех преобразований множества М). Если множество М является непрерывной средой (топологическим пространством), точнее говоря, если известно, что значит
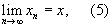
где x1, x2,..., xn,... - некоторая последовательность элементов из М, а x также принадлежит М (как это имеет место, например, в множестве чисел или точек), то можно выделить непрерывные преобразования. Преобразование f называется непрерывным, если из (5) следует
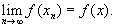
Множество всех непрерывных преобразований составляет группу непрерывных преобразований. Во многих случаях (но не всегда) группа непрерывных преобразований сама естественным образом оказывается непрерывной средой, т. е. в ней определяется понятие предельного перехода: можно говорить о том, что некоторая последовательность преобразований сходится к преобразованию. При этом оказывается, что из
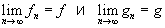
следует

Такая группа называется Н преобразований. Пусть М есть множество точек плоскости. Преобразование f называется движением плоскости, если для каждой пары точек х и у из М расстояние между х и у равно расстоянию между f (x) и f (y). Преобразование плоскости называется проективным, если точки, лежащие на одной прямой, переходят в точки, также лежащие на одной прямой. Частным случаем проективного преобразования является аффинное, при котором параллельные прямые переходят в параллельные. Здесь мы имеем три простейших геометрических примера Н преобразований: группу движений, группу проективных преобразований и группу аффинных преобразований. Если рассматривать те свойства геометрических фигур на плоскости, которые не меняются при движениях плоскости, то мы получим обычную элементарную геометрию. Аналогично возникают геометрии проективная и аффинная, Ф. Клейном была выдвинута общая точка зрения (см. Эрлангенская программа), согласно которой геометрия есть наука, изучающая те свойства фигур, которые не меняются при заданной группе непрерывных преобразований. Отсюда - роль теории Н в геометрии. Примем за множество М всевозможные упорядоченные системы по n чисел x1, x2,..., xn, которые будем трактовать как компоненты вектора х. Рассмотрим т. н. линейное преобразование f, переводящее вектор х в вектор у с компонентами y1, y2,..., yn, причем преобразование задается формулой

Множество всех линейных преобразований составляет Н преобразований. Можно рассматривать не все линейные преобразования, а, например, такие, которые не меняют длины векторов, т. е. для которых выполнено условие
x12 + x22 +... + xn2 = y12 + y22 +... + yn2.
Такие преобразования составляют группу линейных ортогональных преобразований. Группы линейных преобразований играют весьма важную роль, в частности находят свое приложение в квантовой механике.
Современное развитие теории групп показало, что при изучении группы целесообразно бывает отвлечься от того факта, что элементы ее являются преобразованиями, а следует трактовать группу просто как множество элементов, в котором установлена операция умножения, т. е. каждой паре элементов группы поставлен в соответствие элемент, называемый произведением исходных: k = fg, причем в качестве аксиом выдвигаются условия (2), (3), (4). Элемент e, раньше бывший тождественным преобразованием, теперь называется единицей группы. Вместо обратного преобразования появляется обратный элемент. Существование единицы и обратного элемента теперь являются аксиомами. Если для любых двух элементов f и g верно fg = gf, то группа называется коммутативной. Для того чтобы получить Н, следует предположить, что элементы ее составляют топологическое пространство и что операция умножения непрерывна, т. е. выполнено условие (6), которое теперь выдвигается как аксиома. Так возникло в математике новое, абстрактное понятие непрерывной, или, что то же самое, топологической группы. Логически оно слагается из операции перемножения и операции предельного перехода. Так как обе эти операции весьма часто встречаются в математике, то понятие Н принадлежит к числу важных и находит многочисленные приложения. Важнейшим типом Н являются группы Ли (С. Ли - основоположник теории Н). Если в окрестности единицы группы можно ввести координаты, т. е. каждый элемент f задать числами f1, f2,..., fr - его координатами, то закон умножения k = fg можно записать для элементов, близких к единице, в координатной форме:
ki = ji (f1, f2,..., fr, g1, g2,..., gr), (7)
i = 1, 2,..., r,
где ji - непрерывная функция всех переменных. Если еще предположить, что функции j, трижды непрерывно дифференцируемы, то мы придем к понятию группы Ли. Если считать, что координаты единицы все равны нулю, т. е. если принять единицу за начало координат, то, разлагая в ряд Тейлора правую часть соотношения (7), получим
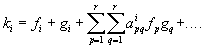
Числа

называются структурными константами группы Ли, и к изучению их полностью сводится изучение группы Ли.
Лит.: Понтрягин Л. С., Непрерывные группы, 3 изд., М., 1973 (имеется библ.).
Л. С. Понтрягин.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 13:22:40
|

|

|
 |
|

|
 |
 |
 |
|