Начертательная геометрия

Начертательная (далее Н) геометрия, раздел геометрии, в котором пространственные фигуры изучаются при помощи построения их изображений на плоскости, в частности построения проекционных изображений, а также методы решения и исследования пространственных задач на плоскости.

Потребность в изображениях пространственных предметов на плоскости возникла в связи с решением различных практических вопросов (например, строительство зданий и других инженерных сооружений, развитие живописи и архитектуры, техники и т.п.). Особенно большое значение имеют чертежи, получаемые проектированием (проецированием) данной фигуры на плоскость (проекционные чертежи). Практика предъявляла к таким чертежам ряд требований; важнейшие из них: 1) наглядность изображения, т. е. свойство чертежа вызывать пространственное представление изображаемой фигуры; 2) "обратимость" чертежа, т. е. возможность точного определения изображенной фигуры по чертежу; 3) простота выполнения требуемых построений; 4) точность графических решений. В способах построения изображений применяются центральное и параллельное проектирование фигуры (натуры, объекта, оригинала) на плоскость проекций (см. Проекция). Наибольшей наглядностью обладают чертежи, полученные способом центрального проектирования, который соответствует геометрической схеме возникновения изображений на сетчатке человеческого глаза. Однако наиболее употребительными в Н геометрия являются параллельные проекции, которые более просты в построении изображений и более удобны для определения по ним натуральной фигуры. Существуют различные виды параллельных проекций; самым распространенным является способ ортогональной проекции на две или три плоскости (комплексный чертеж). Сущность этого способа заключается в следующем. Выбирают две взаимно перпендикулярные плоскости проекций П₁ и П₂ в пространстве. Плоскость П₁ располагают горизонтально; ее называют горизонтально и плоскостью проекций, а плоскость П₂ — фронтальной плоскостью проекций. Произвольную точку А пространства проектируют ортогонально на эти плоскости (рис. 1); получают горизонтальную проекцию A₁ (AA₁(плоскости П₁) и фронтальную проекцию A₂ (AA₂ ^ плоскости П₂). Три точки А, A₁ и A₂ лежат в одной (проектирующей) плоскости, перпендикулярной к линии p₁₂ пересечения плоскостей проекций. Горизонтальную проекцию какой-либо фигуры получают, проектируя ортогонально все точки этой фигуры на плоскость П₁, фронтальную проекцию — на плоскость П₂. Часто бывает полезно добавить третью проекцию фигуры — на плоскость П₃, перпендикулярную к плоскостям П₁ и П₂. Плоскость П₃, а также и проекцию на нее называют профильной. Две проекции точки А (например, A₁ и A₂) вполне определяют третью проекцию (A₃).

Чтобы получить чертеж, состоящий из трех указанных проекций (комплексный чертеж), плоскости П₁ и П₃ совмещают с плоскостью П₂ ("главной" плоскостью) путем вращения их вокруг линий p₁₂ и p₂₃ пересечения этих плоскостей с плоскостью П₂ (рис. 2). Обычно на практике не указывается положение осей проекций p₁₂ и p₁₃, то есть положение плоскостей проекций определяется с точностью до параллельного переноса.

Комплексный чертеж обратим, так как по нему можно определить расстояние между любыми двумя точками натуральной фигуры. Действительно, отрезок AB (рис. 3) в натуре является гипотенузой прямоугольного треугольника ABB*, в котором AB* = A₁₁, а В*В есть разность высот точек В и А, выражаемая на чертеже отрезком ₂*₂. Отсюда можно получить простое построение натурального отрезка

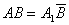
(рис. 4); для этого нужно построить

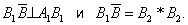
Для увеличения наглядности комплексного чертежа на проекциях фигуры устанавливают "условия видимости": из двух точек А и В, проекции которых на какой-либо из плоскостей проекций совпадают, например A₁ º ₁, видимой считается та, которая расположена ближе к зрителю; "невидимые" линии фигуры условно изображаются штриховыми линиями. Пример такого изображения пространственной фигуры в трех проекциях, называется "вид спереди" (фронтальная проекция), "вид сверху" (горизонтальная проекция) и "вид слева" (профильная проекция), дан на рис. 5.

Комплексный чертеж (из двух или трех ортогональных проекций) является наиболее распространенным видом технического чертежа. По нему легко определяются все необходимые размеры изображаемого предмета. Недостаток таких чертежей — их малая наглядность.

Для построения более наглядных обратимых изображений в Н геометрия применяется другой способ, называемый аксонометрией.

При аксонометрии изображаемую фигуру относят к системе Oxyz осей координат в пространстве (см. Аналитическая геометрия). Эту систему координат называют натуральной. На рис.6 построена координатная ломаная OM_xM₁M для произвольной точки М. Длины координатных отрезков OM_x, M_xM₁, M₁M являются координатами х, у, z точки М. Если спроектировать натуральную систему осей Охуz на плоскость П", то получается так называемая аксонометрическая система осей О"х"у"z" (рис. 6). Проекция "M"_xM"₁M" координатной ломаной состоит из отрезков "M"_x, M"_xM"₁, M"₁M", длины которых x", y", z" в аксонометрической системе координат называется аксонометрическими координатами точки М. Отношения

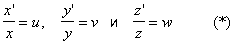
выражают величины искажения координатных отрезков при проектировании; их называют показателями (коэффициентами) искажения. Если все три показателя искажения равны, то аксонометрию называют изометрией, если хотя бы два из них равны — диметрией, если же все показатели искажения неравны — триметрией.

Чтобы при помощи аксонометрического способа построить изображение точки М на плоскости П" в данной параллельной проекции, необходимо иметь: а) натуральные координаты этой точки М (х, у, z); б) аксонометрическую систему осей О"х"у"z" на плоскости проекций П"; в) показатели искажения u, v, w.

Тогда по формулам (*) находят аксонометрические координаты точки М"(х", у", z") и строят по ним точку M", являющуюся искомой проекцией точки М. Аксонометрическое изображение пространственной фигуры строят по точкам, определяющим последнюю. Аксонометрический чертеж обратим: если на аксонометрическом чертеже дана точка M" (х", у", z"), то можно по формулам (*) найти натуральные координаты х, у, z точки М.

Если задать произвольную аксонометрическую систему осей "x"y"z" на плоскости проекций П" (не сводящуюся, однако, к одной прямой) и отношение показателей искажения u: v: w, то, согласно основной теореме аксонометрии (Польке теореме), существует такое положение натуральной системы осей координат относительно плоскости проекций П" и такое направление проектирования, при которых на плоскости П" реализуются ранее выбранная аксонометрическая система осей и отношений показателей искажения.

Для упрощения аксонометрического способа построения изображений пользуются "приведенной" аксонометрией, в которой аксонометрические координаты стремятся по возможности заменить натуральными без искажения вида чертежа. Так, например, на рис. 7 дана ортогональная изометрия объекта, изображенного на комплексном чертеже (рис. 5), с использованием натуральных координат вместо аксонометрических. При этом происходит изменение масштаба аксонометрического чертежа, но вид его сохраняется, т. е. чертеж изменяется подобно. Аксонометрические изображения предметов, не имеющих большого протяжения, обладают достаточной наглядностью. Этого нельзя сказать об изображениях крупных объектов, таких, как здания, плотины и др. сооружения. В этих случаях предпочтительнее применять изображения, выполненные в центральной проекции (перспективе).

Чтобы перспективный чертеж был обратимым, на плоскости проекций П" строят центральную проекцию A" (перспективу) изображаемой точки А и перспективу A₁" ортогональной проекции A₁ точки на горизонтальную плоскость П₁, называемую предметной (рис. 8). Плоскость проекций П" (картинную плоскость) выбирают преимущественно перпендикулярной к предметной. Точка A₁ называется основанием точки А. В частности, ₁ есть основание центра проекций ("глаза") . Зная положение центра относительно картинной плоскости П", можно по данным перспективе A" точки А и перспективе A"₁ ее основания найти положение натуральной точки А в пространстве. Для этого нужно провести SA₁" и найти A₁. Затем построить A₁A ^ плоскости П₁ и найти точку А пересечения прямых SA" и A₁A. Большое значение при построении перспективных изображений имеют т. н. точки схода, являющиеся перспективными изображениями бесконечно удаленных точек пространства, и линия горизонта — перспективное изображение бесконечно удаленной прямой предметной плоскости П₁.

На рис. 9 показано перспективное изображение комнаты. На нем видна главная точка y`_¥, которая является точкой схода для всех прямых, перпендикулярных (в натуре) картинной плоскости, и линия горизонта h. Точки схода др. параллельных прямых, лежащих в предметной плоскости, располагаются на линии горизонта h (например, D"_¥).

Используя координатный метод, можно выполнить построение перспективного изображения по способу центральной аксонометрии, аналогично описанной выше параллельной аксонометрии.

Наряду с построениями перспективных изображений на плоскости (линейная перспектива) на практике употребляются и др. виды центрально-проекционных изображений.

При построении чертежей, изображающих какую-либо часть земной поверхности, удобно пользоваться так называемыми проекциями с числовыми отметками. В этом случае на чертеже должно быть задано достаточное число точек поверхности (рис. 10). Проектируя ортогонально точки поверхности на плоскость проекций, записывают около проекции каждой точки ее высотную отметку, т. е. число, выражающее высоту точки над плоскостью проекций в избранных единицах длины. Благодаря этому такой чертеж является обратимым. Для увеличения его наглядности и удобства пользования, проекции точек, имеющих одинаковую высоту, соединяют линией, которую называют линией уровня. Если изображена земная поверхность, то плоскость проекций считается горизонтальной; линии уровня называют в этом случае горизонталями. По форме и расположению горизонталей можно (с известной степенью точности) судить о рельефе изображенного участка земной поверхности, построить ее сечение заданной на чертеже плоскостью s (рис. 10), а также решать другие задачи. Такой способ изображения поверхности и саму поверхность, заданную системой горизонталей, называют топографическими.

Историческая справка. Первые попытки проекционных изображений можно встретить у древних народов еще до нашей эры. Так, римский архитектор Витрувий в своем сочинении "Десять книг об архитектуре" (1 в. до н. э.) дает понятие о плане (горизонтальной проекции) и фасаде (фронтальной проекции) сооружения. Итальянский архитектор и ученый Л. Альберти (15 в. н. э.) уже применяет "точки схода" и дает важный для практики способ построения перспективы при помощи сетки. В "Трактате о живописи" (опубликован 1651) Леонардо да Винчи имеются многочисленные указания о практических применениях перспективных изображений, в частности о "наблюдательной" перспективе. Немецкий художник А. Дюрер в труде "Руководство к измерению..." (1525) предложил способ построения перспективы по горизонтальной и фронтальной проекциям объекта. Особенно полное изложение приемов построения перспективы были даны итальянским ученым Г. Убальди (1600). Научные основы Н геометрия были разработаны Ж. Дезаргом и главным образом Г. Монжем, который считается создателем научной Н геометрия

В Древней Руси при возведении сооружений применялись изображения, в которых можно заметить элементы геометрического проектирования. Так, изображение города Пскова (1581) было выполнено с соблюдением некоторых законов перспективы. Чертежи изобретателя-самоучки И. П. Кулибина, зодчего Д. В. Ухтомского и др. являются геометрически правильными проекционными изображениями. Курс Н геометрия был впервые введен в 1810 в Петербургском институте корпуса инженеров путей сообщения. Первым русским профессором Н геометрия был Я. А. Севастьянов, написавший ряд сочинений по различным вопросам Н геометрия Научному развитию Н геометрия содействовали геометрические работы Е. С. Федорова, который предложил метод изображения точек пространства на плоскости при помощи векторов. Метод Е. С. Федорова был успешно применен в многомерной Н геометрия, которая используется в физико- анализе (школа Н. С. Курнакова). Советские геометры (А. К. Власов, Н. А. Глаголев, Н. Ф. Четверухин и др.) выполнили ряд исследований в области основной теоремы аксонометрии.

Лит.: Рынин Н. А., Материалы к истории начертательной геометрии, (Библиография, биографии, эпизоды, факты, хронология), Л., 1938; Монж Г., Н геометрия, пер. с (франц.), М., 1947; Федоров Е. С., Новая начертательная геометрия, "Изв. АН", 1917, № 10; Глаголев Н. А., Н геометрия, 3 изд., М., 1953; Вольберг О. А., Лекции по начертательной геометрии, М. — Л., 1947; Курс начертательной геометрии, под ред. Н. Ф. Четверухина, М., 1956; Вопросы современной начертательной геометрии. Сб. ст., под ред. Н. Ф. Четверухина, М. — Л., 1947; Глазунов Е. А. и Четверухин Н. Ф., Аксонометрия, М., 1953: Методы начертательной геометрии и ее приложения. Сб. ст., под ред. Н. Ф. Четверухина, М., 1955; Добряков А. И., Курс начертательной геометрии, 3 изд., М. — Л., 1952.

Н. Ф. Четверухин.

		Новости 21.11.2024 13:16:41

	Copyright © 1999-2024 Oval.ru, All Rights Reserved.