Большая Советская Энциклопедия (цитаты)

Наименьших квадратов метод

Наименьших квадратов метод (далее Н) один из методов ошибок теории для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Н применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается полезным при наблюдений обработке. Н предложен К. Гауссом (1794—95) и А. Лежандром (1805—06). Первоначально Н использовался для обработки результатов астрономических и геодезических наблюдений. Строгое математическое обоснование и установление границ содержательной применимости Н даны А. А. Марковым (старшим) и А. Н. Колмогоровым. Ныне Н представляет собой один из важнейших разделов математической статистики и широко используется для статистических выводов в различных областях науки и техники.

  Сущность обоснования Н (по Гауссу) заключается в допущении, что "убыток" от замены точного (неизвестного) значения физической величины и ее приближенным значением X, вычисленным по результатам наблюдений, пропорционален квадрату ошибки: (X - m)2. В этих условиях оптимальной оценкой естественно признать такую лишенную систематической ошибки величину X, для которой среднее значение "убытка" минимально. Именно это требование и составляет основу Н В общем случае отыскание оптимальной в смысле Н оценки Х — задача весьма сложная, поэтому практически эту задачу сужают и в качестве Х выбирают линейную функцию от результатов наблюдений, лишенную систематической ошибки, и такую, для которой среднее значение "убытка" минимально в классе всех линейных функций. Если случайные ошибки наблюдений подчиняются нормальному распределению и оцениваемая величина m зависит от средних значений результатов наблюдений линейно (случай, весьма часто встречающийся в приложениях Н), то решение этой задачи будет одновременно являться и решением общей задачи. При этом оптимальная оценка Х также подчиняется нормальному распределению со средним значением m и, следовательно, плотность вероятности случайной величины Х



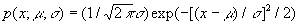
при х = Х достигает максимума в точке m = Х (это свойство и выражает точное содержание распространенного в теории ошибок утверждения "оценка X, вычисленная согласно Н, — наиболее вероятное значение неизвестного параметра m").

  Случай одного неизвестного. Пусть для оценки значения неизвестной величины m произведено n независимых наблюдений, давших результаты 1, 2,..., n, т. е. 1 = m + d1, 2 = m + d2,..., n = m + dn, где d1, d2,..., dn — случайные ошибки (по определению, принятому в классической теории ошибок, случайные ошибки — независимые случайные величины с нулевым математическим ожиданием: Еdi = 0; если же Edi ¹ 0, то Еdi, называются систематическими ошибками). Согласно Н, в качестве оценки величины m принимают такое X, для которого будет наименьшей сумма квадратов (отсюда и само название метода):



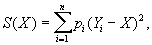
  где pi = k/si2 и si2 = Ddi = Edi2

(коэффициент k > 0 можно выбирать произвольно). Величину pi называют весом, a si — квадратичным отклонением измерения с номером i. В частности, если все измерения равноточны, то s1 = s2 =... = sn, и в этом случае можно положить p1 = p2 =... = pn = 1; если же каждое i, — арифметическое среднее из ni, равноточных измерений, то полагают pi = ni.

  Сумма (X) будет наименьшей, если в качестве Х выбрать взвешенное среднее:



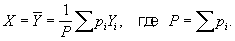
Оценка 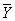 величины m лишена систематической ошибки, имеет вес Р и дисперсию



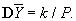
В частности, если все измерения равноточны, то — арифметическое среднее результатов измерений:



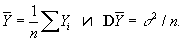
  При некоторых общих предположениях можно показать, что если количество наблюдений n достаточно велико, то распределение оценки 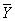 мало отличается от нормального с математическим ожиданием m и дисперсией k/. В этом случае абсолютная погрешность приближенного равенства



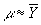
меньше



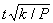
с вероятностью, близкой к значению интеграла



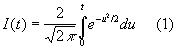
(напр., (1,96) = 0,950; (2,58) = 0,990; (3,00) = 0,997).

  Если веса измерений pi заданы, а множитель k до наблюдений остается неопределенным, то этот множитель и дисперсия оценки 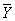 могут быть приближенно оценены по формулам:



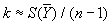
и



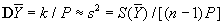
(обе оценки лишены систематических ошибок).

  В том практически важном случае, когда ошибки di подчиняются нормальному распределению, можно найти точное значение вероятности, с которой абсолютная погрешность приближенного равенства



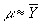
окажется меньше ts (t — произвольное положительное число). Эту вероятность, как функцию от t, называют функцией распределения Стьюдента с n - 1 степенями свободы и вычисляют по формуле



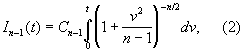
где постоянная n-1 выбрана таким образом, чтобы выполнялось условие: n-1(¥) = 1. При больших n формулу (2) можно заменить формулой (1). Однако применение формулы (1) при небольших n привело бы к грубым ошибкам. Так, например, согласно (1), значению = 0,99 соответствует t = 2,58; истинные значения t, определяемые при малых n как решения соответствующих уравнений ln-1(t) = 0,99, приведены в таблице:

n
2
3
4
5
10
20
30

t
63,66
9,92
5,84
4,60
3,25
2,86
2,76

Пример. Для определения массы некоторого тела произведено 10 независимых равноточных взвешиваний, давших результаты i (в г):

i
18,41
18,42
18,43
18,44
18,45
18,46

ni
1
3
3
1
1
1

(здесь ni — число случаев, в которых наблюдался вес i, причем n = ni, = 10). Так как все взвешивания равноточные, то следует положить pi = ni и в качестве оценки для неизвестного веса m, выбрать величину



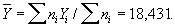
Задавая, например, 9 = 0,95, по таблицам распределения Стьюдента с девятью степенями свободы можно найти, что t = 2,262, и поэтому в качестве предельной абсолютной погрешности приближенного равенства m " 18,431 следует принять величину



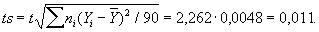
  Т. о. 18,420 < m < 18,442.

  Случай нескольких неизвестных (линейные связи). Пусть n результатов измерений 1, 2,..., n связаны с m неизвестными величинами x1, x2,..., хm (m < n) независимыми линейными отношениями



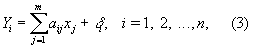
где aij — известные коэффициенты, а di — независимые случайные ошибки измерений. Требуется оценить неизвестные величины xj (эту задачу можно рассматривать как обобщение предыдущей, в которой m = x1 и m = ai1 = 1; i = 1,2,..., n).

  Так как Еdi = 0, то средние значения результатов измерений yi, = Eyi. связаны с неизвестными величинами x1, x2,..., хm линейными уравнениями (линейные связи):



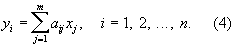
  Следовательно, искомые величины xj представляют собой решение системы (4), уравнения которой предполагаются совместными. Точные значения измеряемых величин yi и случайные ошибки di обычно неизвестны, поэтому вместо систем (3) и (4) принято записывать так называемые условные уравнения



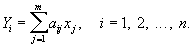
  Согласно Н, качестве оценок для неизвестных xj применяют такие величины Xj, для которых сумма квадратов отклонений



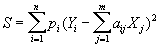
будет наименьшей (как и в предыдущем случае, pi — вес измерения i, — величина, обратно пропорциональная дисперсии случайной ошибки di). Условные уравнения, как правило, несовместны, т. е. при любых значениях Xj разности



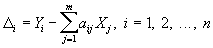
не могут, вообще говоря, все обратиться в нуль, и в этом случае



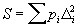
также не может обратиться в нуль. Н предписывает в качестве оценок выбрать такие значения Xj, которые минимизируют сумму . В тех исключительных случаях, когда условные уравнения совместны и, значит, обладают решением, это решение совпадает с оценками, полученными согласно Н

  Сумма квадратов представляет собой квадратичный многочлен относительно переменных Xj; этот многочлен достигает минимума при таких значениях X1, X2,..., Хm, при которых обращаются в нуль все первые частные производные:



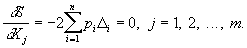
Отсюда следует, что оценки Xj, полученные согласно Н, должны удовлетворять системе так называемых нормальных уравнений, которая в обозначениях, предложенных Гауссом, имеет вид:



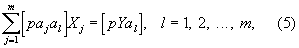
где



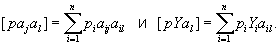
  Оценки Xj, получающиеся в результате решения системы нормальных уравнений, лишены систематических ошибок (Exj = xj); дисперсии Dxj; величин Xj равны kdjj/d, где d — определитель системы (5), а djj — минор, соответствующий диагональному элементу (раjaj) (иными словами, djj/d — вес оценки Xj). Если множитель пропорциональности k (k называется дисперсией на единицу веса) заранее неизвестен, то для его оценки, а также для оценки дисперсии Dxj служат формулы:

  k " /(n - m) и Dxj " s2j = Sdjj/d (n - m)

( — минимальное значение исходной суммы квадратов). При некоторых общих предположениях можно показать, что если количество наблюдений n достаточно велико, то абсолютная погрешность приближенного равенства xi " Xj меньше tsj с вероятностью, близкой к значению интеграла (1). Если случайные ошибки наблюдений di подчиняются нормальному распределению, то все отношения (Xj - xj)/sj распределены по закону Стьюдента с n - m степенями свободы (точная оценка абсолютной погрешности приближенного равенства производится здесь с помощью интеграла (2) так же, как в случае одного неизвестного). Кроме того, минимальное значение суммы в вероятностном смысле не зависит от X1, X2,..., Xm и поэтому приближенные значения дисперсий оценок Dxj " s2j не зависят от самих оценок Xj.

  Один из наиболее типичных случаев применения Н — "выравнивание" таких результатов наблюдений i, для которых в уравнениях (3) aij = aj (ti), где aj (t) — известные функции некоторого параметра t (если t — время, то t1, t2,... — те моменты времени, в которые производились наблюдения). Особенно часто встречается в приложениях случай так называемой параболической интерполяции, когда aj (t) — многочлены (например, a1(t) = 1, a2(t) = t, a3(t) = t2,... и т.д.); если t2 — t1 = t3 — t2 =... = tn — tn-1, a наблюдения равноточные, то для вычисления оценок Xj можно воспользоваться таблицами ортогональных многочленов, имеющимися во многих руководствах по современной вычислительной математике. Другой важный для приложения случай — так называемая гармоническая интерполяция, когда в качестве aj (t) выбирают тригонометрические функции (например, aj (t) = cos (j - 1) t, j = 1, 2,..., m).

  Пример. Для оценки точности одного из методов анализа этим методом определялась концентрация в десяти эталонных пробах заранее известного состава. Результаты равноточных наблюдений указаны в таблице (i — номер эксперимента, ti — истинная концентрация , Ti — концентрация . определенная в результате анализа, i = Ti - ti — ошибка анализа):

i
1
2
3
4
5
6
7
8
9
10

ti
4
8
12,5
16
20
25
31
36
40
40

i
- 0,3
- 0,2
- 0,4
- 0,4
- 0,2
- 0,5
+ 0,1
- 0,5
-0,6
-0,5


Если результаты анализа не имеют систематических ошибок, то Eyi = 0. Если же такие ошибки имеются, то в первом приближении их можно представить в виде: Eyi = a + bti (a называется постоянной ошибкой, а bti — методической ошибкой) или, что то же самое,



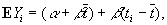
где



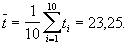
  Для отыскания оценок a и b достаточно оценить коэффициенты



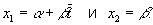
Условные уравнения в данном случае имеют вид:



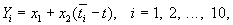
поэтому ai1 = 1, ai2 = ti - t (согласно предположению о равноточности наблюдений, все pi = 1). Так как



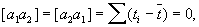
то система нормальных уравнений записывается особенно просто:

(a1a1) X1 = (Ya1); (a2a2) X2 = (Ya2),

где



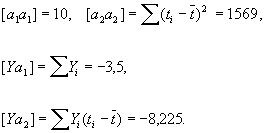
  Дисперсии компонент решения этой системы суть



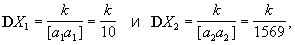
где k — неизвестная дисперсия на единицу веса (в данном случае k — дисперсия любой из величин i). Так как в этом примере компоненты решения принимают значения X1 = -0,35 и X2 = -0,00524, то



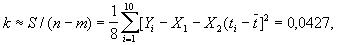
  Dx1 " s12 = 0,00427,

  Dx2 " s22 = 0,0000272,

  s1 = 0,065, s2 = 0,00522.

  Если случайные ошибки наблюдений подчиняются нормальному распределению, то отношения |Xj – xjl/sj (j = 1, 2) распределены по закону Стьюдента. В частности, если результаты наблюдений лишены систематических ошибок, то x1 = x2 = 0 и, значит, закону Стьюдента должны подчиняться отношения |X1|/s1 и |X2|/s2. С помощью таблиц распределения Стьюдента с n – m = 8 степенями свободы можно убедиться, что если действительно x1 = x2 = 0, то с вероятностью 0,999 каждое из этих отношений не должно превосходить 5,04 и с вероятностью 0,95 не должно превосходить 2,31. В данном случае |X1|/s1 = 5,38 > 5,04, поэтому гипотезу отсутствия систематических ошибок целесообразно отвергнуть; в то же время следует признать, что гипотеза об отсутствии методической ошибки (x2 = 0) не противоречит результатам наблюдений, так как |X2|/s2 = 1,004 < 2,31. Т. о., можно заключить, что для определения t по результату наблюдения Т целесообразно пользоваться приближенной формулой t = Т + 0,35.

  Во многих практически важных случаях (и в частности, при оценке сложных нелинейных связей) количество неизвестных параметров бывает весьма большим и поэтому реализация Н оказывается эффективной лишь при использовании современной вычислительной техники.

  Лит.: Марков А. А., Исчисление вероятностей, 4 изд., М., 1924; Колмогоров А. Н., К обоснованию метода наименьших квадратов, "Успехи математических наук", 1946, т. 1, в. 1; Линник Ю. В., Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений, 2 изд., М., 1962; Helmert . R., Die Ausgieichungsrechnung nach der Methode der kleinsten Quadrate..., 2 Aufl., Lpz., 1907.

  Л. Н. Большев.

 


Для поиска, наберите искомое слово (или его часть) в поле поиска

Новости 21.11.2024 13:39:37

     Copyright © 1999-2024 Oval.ru, All Rights Reserved.