Момент

Момент (далее М) (лат. momentum - движущая сила, толчок, побудительное начало, от moveo - двигаю), математическое понятие, играющее важную роль в механике и теории вероятностей. 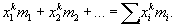Если на прямой линии расположена система материальных точек, массы которых соответственно равны m1, m2, ..., (mi > 0), а абсциссы относительно некоторого начала отсчета О равны x1, x2, ..., то мо ментом порядка k этой системы относительно точки О называют сумму М первого порядка в механике называется статическим моментом, а М второго порядка - моментом инерции. Если в выражении М все абсциссы заменить их абсолютными значениями, то получатся т. н. абсолютные М Точку с абсциссой (iximi)/(imi) называются центром данной системы масс. М, вычисленные относительно центра, называются центральными. Центральный М первого порядка для всякой системы равен нулю. Из всех М инерции центральный является наименьшим. Неравенство Чебышева: сумма масс, находящихся от точки О на расстоянии, большем а, не превышает М инерции системы относительно О, разделенного на а2.   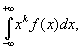Если распределение массы имеет плотность f(x) ³ 0, то М порядка k называют интеграл при условии его абсолютной сходимости. В случае произвольно распределенной массы, суммы в выражениях для М заменяются интегралами Стилтьеса (см. Интеграл); именно таким путем и возник впервые интеграл Стилтьеса. Все упомянутые определения и теоремы при этом сохраняют силу.   В теории вероятностей роль абсцисс играют различные возможные значения случайной величины, а на места масс становятся соответствующие вероятности. М первого порядка (который здесь всегда является абсциссой центра, т. к. полная масса равна 1) называются математическим ожиданием данной случайной величины, а центральный М второго порядка - ее дисперсией. В теории вероятностей чрезвычайно важную роль играет упомянутое неравенство Чебышева. В математической статистике М служат обычно основными статистическими сводными характеристиками распределений.   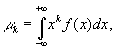Задача математического анализа, состоящая в том, чтобы охарактеризовать свойства функции f(x) по свойствам последовательности ее М: носит название проблемы моментов. Эта задача впервые рассматривалась П. Л. Чебышевым в 1874 в связи с исследованиями по теории вероятностей (попытка доказать центральную предельную теорему). Позже при исследовании этой задачи возникли новые мощные методы математического анализа.   Лит.: Чебышев П. Л., Избр. труды, М, 1955; Марков А. А., Избр. труды, М, 1951; Гнеденко Б. В., Курс теории вероятностей, 5 изд., М, 1969; Лоэв М, Теория вероятностей, пер. с англ., М, 1962.