|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Многочлен | Многочлен (далее М) полином, выражение вида
Axkyl…..wm + Bxnyp…..wq + …… + Dxrts…..wt,
где х, у, ..., w — переменные, а А, В, ..., D (коэффициенты М) и k, l, ..., t (показатели степеней — целые неотрицательные числа) — постоянные. Отдельные слагаемые вида Ахkyl…..wm называются членами М Порядок членов, а также порядок множителей в каждом члене можно менять произвольно; точно так же можно вводить или опускать члены с нулевыми коэффициентами, а в каждом отдельном члене — степени с нулевыми показателями. В случае, когда М имеет один, два или три члена, его называют одночленом, двучленом или трехчленом. Два члена М называются подобными, если в них показатели степеней при одинаковых переменных попарно равны. Подобные между собой члены
А"хkyl…..wm, "xkyl…..wm, ….., D"xkyl…..wm
можно заменить одним (приведение подобных членов). Два М называются равными, если после приведения подобных все члены с отличными от нуля коэффициентами оказываются попарно одинаковыми (но, может быть, записанными в разном порядке), а также если все коэффициенты этих М оказываются равными нулю. В последнем случае М называется тождественным нулем и обозначают знаком 0. М от одного переменного х можно всегда записать в виде
(x) = a0xn + a1xn-1 + ... + an-1x + an,
где a0, a1,..., an — коэффициенты.
Сумму показателей степеней какого-либо члена М называют степенью этого члена. Если М не тождественный нуль, то среди членов с отличными от нуля коэффициентами (предполагается, что все подобные члены приведены) имеются один или несколько наибольшей степени; эту наибольшую степень называют степенью М Тождественный нуль не имеет степени. М нулевой степени сводится к одному члену А (постоянному, не равному нулю). Примеры: xyz + х + у + z есть многочлен третьей степени, 2x + у — z + 1 есть многочлен первой степени (линейный М), 5x2 — 2x2 — 3х2 не имеет степени, т. к. это тождественный нуль. М, все члены которого одинаковой степени, называется однородным М, или формой; формы первой, второй и третьей степеней называются линейными, квадратичными, кубичными, а по числу переменных (два, три) двоичными (бинарными), тройничными (тернарными) (например, x2 + y2 + z2 — ху — yz — xz есть тройничная квадратичная форма).
Относительно коэффициентов М предполагается, что они принадлежат определенному полю (см. Поле алгебраическое), например полю рациональных, действительных или комплексных чисел. Выполняя над М действия сложения, вычитания и умножения на основании переместительного, сочетательного и распределительного законов, получают снова М Таким образом, совокупность всех М с коэффициентами из данного поля образует кольцо (см. Кольцо алгебраическое) — кольцо многочленов над данным полем; это кольцо не имеет делителей нуля, т. е. произведение М, не равных 0, не может дать 0.
Если для двух многочленов Р(х) и Q(x) можно найти такой многочлен R(x), что Р = QR, то говорят, что Р делится на Q; Q называется делителем, a R — частным. Если Р не делится на Q, то можно найти такие многочлены Р(х) и (x), что Р = QR + , причем степень (x) меньше степени Q(x).
Посредством повторного применения этой операции можно находить наибольший общий делитель Р и Q, т. е. такой делитель Р и Q, который делится на любой общий делитель этих многочленов (см. Евклида алгоритм). М, который можно представить в виде произведения М низших степеней с коэффициентами из данного поля, называется приводимым (в данном поле), в противном случае — неприводимым. Неприводимые М играют в кольце М роль, сходную с простыми числами в теории целых чисел. Так, например, верна теорема: если произведение PQ делится на неприводимый многочлен R, a на R не делится, то тогда Q должно делиться на R. Каждый М степени, большей нуля, разлагается в данном поле в произведение неприводимых множителей единственным образом (с точностью до множителей нулевой степени). Например, многочлен x4 + 1, неприводимый в поле рациональных чисел, разлагается на два множителя
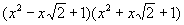
в поле действительных чисел и на четыре множителя 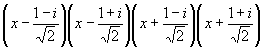 в поле комплексных чисел. Вообще каждый М от одного переменного х разлагается в поле действительных чисел на множители первой и второй степени, в поле комплексных чисел — на множители первой степени (основная теорема алгебры). Для двух и большего числа переменных этого уже нельзя утверждать; например, многочлен x3 + yz2 + z3 неприводим в любом числовом поле.
Если переменным х, у, ..., w придать определенные числовые значения (например, действительные или комплексные), то М также получит определенное числовое значение. Отсюда следует, что каждый М можно рассматривать как функцию соответствующих переменных. Эта функция непрерывна и дифференцируема при любых значениях переменных; ее можно характеризовать как целую рациональную функцию, т. е. функцию, получающуюся из переменных и некоторых постоянных (коэффициентов) посредством выполненных в определенном порядке действий сложения, вычитания и умножения. Целые рациональные функции входят в более широкий класс рациональных функций, где к перечисленным действиям присоединяется деление: любую рациональную функцию можно представить в виде частного двух М Наконец, рациональные функции содержатся в классе алгебраических функций.
К числу важнейших свойств М относится то, что любую непрерывную функцию можно с произвольно малой ошибкой заменить М (теорема Вейерштрасса; точная ее формулировка требует, чтобы данная функция была непрерывна на каком-либо ограниченном, замкнутом множестве точек, например на отрезке числовой оси). Этот факт, доказываемый средствами математического анализа, дает возможность приближенно выражать М любую связь между величинами, изучаемую в каком-либо вопросе естествознания и техники. Способы такого выражения исследуются в специальных разделах математики (см. Приближение и интерполирование функций, Наименьших квадратов метод).
В элементарной алгебре многочленом иногда называются такие алгебраические выражения, в которых последним действием является сложение или вычитание, например
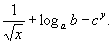
Лит. : Курош А. Г., Курс высшей алгебры, 9 изд., М, 1968; Мишина А. П., Проскуряков И. В., Высшая алгебра, 2 изд., М, 1965.
А. И. Маркушевич.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 21.11.2024 11:37:32
|
|
|
|
|
|
|
|
|
|
|
