
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Минимальные поверхности | Минимальные поверхности (далее М)поверхности, у которых средняя кривизна во всех точках равна нулю (см. Кривизна). Минимальные поверхности появляются при решении следующей вариационной задачи: в пространстве дана некоторая замкнутая кривая; среди всех возможных поверхностей, проходящих через эту кривую, найти такую, для которой часть ее, заключенная внутри кривой, имела бы наименьшую площадь (минимальную площадь - отсюда название). Если заданная кривая - плоская, то решением, очевидно, будет ограниченный этой кривой кусок плоскости. В случае неплоской кривой необходимое условие, которому должна удовлетворять поверхность с минимальной площадью, было установлено Ж. Лагранжем в 1760 и несколько позже истолковано геометрически Ж. Менье в форме, эквивалентной требованию, чтобы средняя кривизна обращалась в нуль. Хотя это условие не является достаточным, т. е. не гарантирует минимума площади, однако впоследствии название "Минимальные поверхности" было сохранено за всякой поверхностью с нулевой средней кривизной. Если предположить поверхность заданной уравнением z = f (х, у), то, приравнивая нулю выражение для средней кривизны, приходят к дифференциальному уравнению с частными производными 2-го порядка:
(1 + q2)r - 2pqs + (1 + p2)t = 0,
где
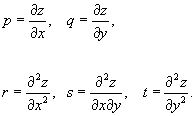
Исследованием этого уравнения в различных формах занимались многие математики, начиная с Ж. Лагранжа и Г. Монжа. Примерами Минимальные поверхности могут служить: обыкновенная винтовая поверхность; катеноид - единственная (вещественная) Минимальные поверхности среди поверхностей вращения; "поверхность Шерка", определяемая уравнением
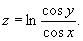
Минимальные поверхности имеет во всех точках неположительную полную кривизну. Бельгийский физик Ж. Плато предложил способ экспериментального осуществления Минимальные поверхности при помощи мыльных пленок, натянутых на проволочный каркас.
Лит.: Каган В. Ф., Основы теории поверхностей в тензорном изложении, ч. 1, М. - Л., 1947; Курант Р., Роббинс Г., Что такое математика, пер. с англ., 2 изд., М., 1967; Бляшке В., Введение в дифференциальную геометрию, пер. с нем., М., 1957.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 12:04:50
|

|

|
 |
|

|
 |
 |
 |
|