
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Линия (геометрич. понятие) | Линия (далее Л) (от лат. linea), геометрическое понятие, точное и в то же время достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах геометрии различно.
1) В элементарной геометрии рассматриваются прямые Л (геометрич. понятие), отрезки прямых, ломаные Л (геометрич. понятие), составленные из отрезков, и некоторые кривые Л (геометрич. понятие) Каждый вид кривых Л (геометрич. понятие) определяется тем или иным специальным способом (например, окружность определяется как геометрическое место точек, имеющих заданное расстояние R от заданной точки О — центра окружности). Иногда в учебниках дают определение Л (геометрич. понятие) как границы куска поверхности (поверхность определяется при этом как граница тела) или как траектории движущейся точки. Но в рамках элементарной геометрии эти определения не получают отчетливой формулировки.
2) Представление о Л (геометрич. понятие) как траектории движущейся точки может быть сделано вполне строгим при помощи идеи параметрического представления Л (геометрич. понятие) Например, вводя на плоскости прямоугольные координаты (x, у), можно параметрически задать окружность радиуса R с центром в начале координат уравнениями
x = R cos t, y = R sin t.
Когда параметр t пробегает отрезок 0 £ t £ 2p, точка (х, у) описывает окружность. Вообще, Л (геометрич. понятие) на плоскости задают параметрическими уравнениями вида
x = j (t), у = 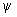 (t), (t),
где j (t), 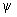 (t) — произвольные функции, непрерывные на каком-нибудь конечном или бесконечном интервале D числовой оси t. С каждым значением параметра t (из интервала D) уравнения (*) сопоставляют некоторую точку M, координаты которой определяются этими уравнениями. Л (геометрич. понятие), заданная параметрическими уравнениями (*) есть множество точек, соответствующих всевозможным значениям t из D, при условии, что эти точки рассматриваются в определенном порядке, именно: если точка M1 соответствует значению параметра t1, а точка M2 — значению t2, то M1 считается предшествующей M2, если t1 < t2 При этом точки, отвечающие различным значениям параметра, всегда считаются различными. (t) — произвольные функции, непрерывные на каком-нибудь конечном или бесконечном интервале D числовой оси t. С каждым значением параметра t (из интервала D) уравнения (*) сопоставляют некоторую точку M, координаты которой определяются этими уравнениями. Л (геометрич. понятие), заданная параметрическими уравнениями (*) есть множество точек, соответствующих всевозможным значениям t из D, при условии, что эти точки рассматриваются в определенном порядке, именно: если точка M1 соответствует значению параметра t1, а точка M2 — значению t2, то M1 считается предшествующей M2, если t1 < t2 При этом точки, отвечающие различным значениям параметра, всегда считаются различными.
Аналогично, в трехмерном пространстве Л (геометрич. понятие) задается параметрически тремя уравнениями вида
x = j (t), у = 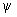 (t), z = c (t), (t), z = c (t),
где j (t), 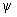 (t), c (t) — произвольные функции, непрерывные на каком-нибудь интервале. В произвольном топологическом пространстве Т (которое, в частности, может быть плоскостью, поверхностью, обычным трехмерным пространством, функциональным пространством и т. п.) Л (геометрич. понятие) параметрически задают уравнением вида (t), c (t) — произвольные функции, непрерывные на каком-нибудь интервале. В произвольном топологическом пространстве Т (которое, в частности, может быть плоскостью, поверхностью, обычным трехмерным пространством, функциональным пространством и т. п.) Л (геометрич. понятие) параметрически задают уравнением вида
= j (t),
где j — функция действительного переменного t, непрерывная на каком-либо интервале, значения которой суть точки пространства Т. Считают, что два параметрических представления задают одну и ту же Л (геометрич. понятие), если они определяют один и тот же порядок следования ее точек (в смысле, указанном выше).
В анализе и топологии рассматривают обычно случай, когда область изменения параметра t есть отрезок а £ t £ b. В этом случае условие того, чтобы два параметрических представления
Р = j (t), a £ t £ b
= j1(t1), a1 £ t1 £ b1,
изображали одну и ту же Л (геометрич. понятие), заключается в существовании непрерывной и строго возрастающей функции
t1 = f(t),
для которой
f(a) = a1, f(b) = b1, j (t) = j1(f(t)).
Такое понимание термина "Л (геометрич. понятие)" наиболее естественно в большинстве вопросов анализа (например, в теории криволинейных интегралов) и механики. Так как Л (геометрич. понятие) здесь рассматривается вместе с порядком, в котором пробегает ее точки переменная точка М при возрастании t, то при этом естественно возникает вопрос о числе прохождений переменной точки Л (геометрич. понятие) через какую-либо точку пространства. Кроме простых точек, проходимых один раз, Л (геометрич. понятие) может иметь кратные точки, которые проходятся несколько раз (отвечающие различным значениям параметра).
Например, при изменении t в пределах — ¥ < t < ¥ точка с координатами
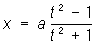 , , 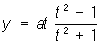
описывает строфоиду (см. рис. "Алгебраические кривые третьего порядка", № 5), попадая в положение х = 0, у = 0 два раза при t = — 1 и t = + 1.
3) Из аналитической геометрии известен и другой способ задания Л (геометрич. понятие) на плоскости уравнением
(x, y) = 0;
в пространстве — двумя уравнениями
(x, у, z) = 0, G(x, y, z) = 0.
Ограничиваясь случаем плоскости, укажем лишь, как строится понятие алгебраической Л (геометрич. понятие) (кривой) — Л (геометрич. понятие), определяемой уравнением
(x, y) = 0,
где (x, у) — целая алгебраическая функция, т. е. многочлен како-либо степени n ³ 1. В этом случае считают, что два многочлена 1(x, у) и 2(x, у) определяют одну и ту же алгебраическую Л (геометрич. понятие) в том и только в том случае, когда существует такая постоянная с ¹ 0, что выполняется тождественно соотношение
1(x, y) = cF2(x, у).
Таким образом, все многочлены, определяющие одну и ту же Л (геометрич. понятие), имеют одну и ту же степень n, называемую порядком соответствующей Л (геометрич. понятие) Например, в аналитической геометрии принято считать, что уравнение
(х - у)2 = 0
определяет Л (геометрич. понятие) второго порядка, а именно, дважды взятую прямую х — у = 0.
В связи с последним примером необходимо заметить, однако, что часто целесообразно ограничиваться рассмотрением неприводимых алгебраических Л (геометрич. понятие), т. е. таких Л (геометрич. понятие), для которых многочлен не допускает представления = GH, где G и Н — отличные от постоянных многочлены. Далее, в пункте 4, имеется в виду только этот случай.
Говорят, что точка (x0, y0) кривой (x, у) = 0 имеет кратность m, если разложение (x, у) по степеням x = х — x0, h = у — y0 начинается с членов степени m (по совокупности переменных x и h). В случае m = 2, т. е. в случае двойной точки
(x, у) = а11(х — x0)2 + 2а12(х — x0) (у — y0) + a22(y — y0)2 + ...,
где многоточие означает, что далее следуют члены высших порядков. При помощи дискриминанта
d = a11a22 — а122
можно определить тип двойной точки (см. Особые точки).
4) Часто, особенно при изучении алгебраической Л (геометрич. понятие), целесообразно стать на точку зрения комплексной проективной геометрии, т. е. рассматривать, наряду с точками евклидовой действительной плоскости (или пространства), точки бесконечно удаленные и мнимые. Только при таком подходе (и надлежащем учете кратности пересечения) становится верным, например, утверждение, что две Л (геометрич. понятие) порядков n и m пересекаются в mn точках. В случае m = 1 это приводит к возможности определить порядок Л (геометрич. понятие) как число n точек ее пересечения с прямой.
С проективной точки зрения естественно задавать Л (геометрич. понятие) на плоскости однородным уравнением
(x1, x2, x3) = 0
между однородными координатами x1, x2, x3 ее точек. В силу принципа двойственности с этим заданием равноправно задание Л (геометрич. понятие) уравнением
(x1, x2, x3) = 0,
связывающим однородные координаты прямых, касающихся Л (геометрич. понятие) Таким образом, наряду с порядком Л (геометрич. понятие) (степенью уравнения = 0) естественно возникает понятие класса Л (геометрич. понятие) — степени уравнения = 0. Класс алгебраических Л (геометрич. понятие) можно также определить как число касательных, которые можно провести к Л (геометрич. понятие) из произвольной точки. О параметрическом представлении Л (геометрич. понятие) см. также Уникурсальные кривые.
5) Рассмотренные выше (в пунктах 2—4) уточнения и обобщения понятия Л (геометрич. понятие) существенно связаны с соответствующим алгебраическим и аналитическим аппаратом. В отличие от этого, современная топология выдвинула задачу уточнения представления о Л (геометрич. понятие) как о множестве точек, независимо от алгебраического или аналитического способов задания этого множества.
Если исходить из параметрического задания Л (геометрич. понятие) в виде непрерывной функции = j (t), где t пробегает отрезок а £ t £ b, но интересоваться только полученным множеством точек без учета порядка их следования, то приходят к понятию Л (геометрич. понятие), сформулированному в 80-x гг. 19 в. К. Жорданом (см. Жордана кривая). Оказывается, что таким непрерывным образом отрезка может быть любой локально связный континуум, в частности квадрат, треугольник, куб и т. п. (см. Пеано кривая). Поэтому теперь обычно предпочитают говорить не о Л (геометрич. понятие) в смысле Жордана, а о локально связных, или жордановых, континуумах. Взаимно однозначный непрерывный образ отрезка называют простой дугой, или жордановой дугой. Взаимно однозначный непрерывный образ окружности называют простой замкнутой Л (геометрич. понятие) Простые дуги и простые замкнутые Л (геометрич. понятие) не исчерпывают, однако, точечных множеств, заслуживающих наименования Л (геометрич. понятие)
Избегая и чрезмерной общности, и чрезмерного сужения понятия Л (геометрич. понятие), в современной топологии пользуются понятием Л (геометрич. понятие), введенным в 1921 П. С. Урысоном, который определяет Л (геометрич. понятие) (кривую) как произвольный континуум размерности единица. Континуум имеет размерность единица, если при любом e > 0 он может быть представлен в виде суммы конечного числа замкнутых множеств диаметра, меньшего e, обладающих тем свойством, что никакие три из этих замкнутых множеств не имеют общей точки (см. также Размерность в геометрии). Континуум, лежащий на плоскости, будет Л (геометрич. понятие) в смысле Урысона тогда и только тогда, когда он не содержит внутренних точек. Этим свойством характеризовал ранее (70-е гг. 19 в.) Л (геометрич. понятие), лежащие на плоскости, Г. Кантор. Хотя определение Кантора применимо только к Л (геометрич. понятие), лежащим на плоскости, иногда и общие Л (геометрич. понятие) в смысле Урысона называют "канторовыми кривыми".
Л (геометрич. понятие) Н. Колмогоров.
6) Еще математики древности изучали линии второго порядка (эллипс, гиперболу и параболу). Ими же был рассмотрен ряд отдельных замечательных алгебраических Л (геометрич. понятие) более высокого порядка, а также некоторые трансцендентные (неалгебраические) Л (геометрич. понятие) Систематическое изучение Л (геометрич. понятие) и их классификация стали возможными с созданием аналитической геометрии (Р. Декарт).
Из Л (геометрич. понятие) третьего порядка наиболее известны:
Декартов лист (см. рис. "Алгебраические кривые третьего порядка", № 1). уравнение в прямоугольных координатах: x3 + y3 — 3аху = 0. Впервые кривая определяется в письме Р. Декарта к П. Ферма в 1638. Полная форма кривой с наличием асимптоты, проходящей через точки ( —а, 0) и (0, —а), была определена позднее (1692) Х. Гюйгенсом и И. Бернулли. Название "декартов лист" установилось в начале 18 в.
Локон Аньези (см. рис. "Алгебраические кривые третьего порядка", № 2). Пусть имеется круг с диаметром = -а и отрезок BDM, построенный так, что ОВ : BD = : ВМ; геометрическое место точек М представляет собой локон Аньези (или верзиеру). уравнение в прямоугольных координатах: у = a3/(a2 + x2). Исследование этой Л (геометрич. понятие) связано с именем итальянской женщины-математика Марии Аньези (1748).
Кубическая парабола (см. рис. "Алгебраические кривые третьего порядка", № 3). уравнение в прямоугольных координатах: у = x3.
Полукубическая парабола (см. рис. "Алгебраические кривые третьего порядка", № 4), парабола Нейля. уравнение в прямоугольных координатах: у = -сх3/2. Названа по имени английского математика У. Нейля (1657), нашедшего длину ее дуги.
Строфоида (от греч. stróphos — крученая лента и éidos — вид) (см. рис. "Алгебраические кривые третьего порядка", № 5). Пусть имеется неподвижная прямая АВ и точка С вне ее на расстоянии = а; вокруг С вращается прямая, пересекающая АВ в переменной точке . Если от точки отложить по обе стороны прямой АВ отрезки NM = NM" = , то геометрическое место точек М и М" для всех положений вращающегося луча и есть строфоида. Уравнение в прямоугольных координатах: 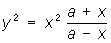 ; в полярных координатах: r = —a cos 2j/cosj. Впервые строфоиду исследовал Э. Торричелли (1645), название было введено в середине 19 в. ; в полярных координатах: r = —a cos 2j/cosj. Впервые строфоиду исследовал Э. Торричелли (1645), название было введено в середине 19 в.
Циссоида Диоклеса (см. рис. "Алгебраические кривые третьего порядка", № 6) (греч. kissoeides, от kissós — плющ и éidos — вид), геометрическое место точек М, для которых OM = PQ (Р — произвольная точка производящего круга с диаметром а). Уравнение в прямоугольных координатах: y2 = х3/(а — х); в полярных координатах: r = asin2 j/cos j. Древние греки рассматривали только ту часть циссоиды, которая находится внутри производящего круга. Вместе с дугой окружности эта часть образует фигуру, напоминающую лист плюща (откуда название); наличие бесконечных ветвей было установлено в 17 в. французским математиком Ж. П. Робервалем и независимо от него бельгийским математиком Р. Ф. Слюзом.
Из Л (геометрич. понятие) четвертого и более высоких порядков наиболее известны:
Кардиоида (от греч. kardía — сердце и éidos — вид) (см. рис. "Алгебраические кривые четвертого и более высоких порядков", № 1), кривая, описываемая какой-либо точкой М окружности радиуса а, катящейся без скольжения по неподвижной окружности того же радиуса. уравнение в прямоугольных координатах: (x2 + y2 — 2ах)2 = 4a(x2 + y2); в полярных координатах: r = 2а (1 + cos j).
Конхоида Никомеда (от греч. konchoeides — похожий на раковину) (см. рис. "Алгебраические кривые четвертого и более высоких порядков", № 2), кривая, получающаяся при увеличении или уменьшении каждого радиус-вектора точек данной прямой на одну и ту же величину d, т. о., OM = — d или OM" = + d. Если расстояние от полюса О до данной прямой равно а, то уравнение в прямоугольных координатах: (х — а)2(х2 + y2) — d2x2 = 0, в полярных координатах: r = a/cosj ± d. Впервые рассматривалась древнегреческим геометром Никомедом (около 250—150 до нашей эры), который использовал ее для решения задач о трисекции угла и удвоении куба.
Лемниската Бернулли (см. рис. "Алгебраические кривые четвертого и более высоких порядков", № 3) (от лат. lemniscatus, буквально — украшенный лентами), кривая, имеющая форму восьмерки; геометрическое место точек, произведение расстояний которых от фокусов 1 ( — а, 0) и 2 (а, 0) равно а2. уравнение в прямоугольных координатах: (x2 + y2)2 — 2a2 (x2 — y2) =0, в полярных координатах: r2 = 2а2 cos 2j. Впервые рассматривалась Я. Бернулли (1694). Лемниската является частным случаем овалов Кассини и синус-спиралей.
Овалы Декарта (см. рис. "Алгебраические кривые четвертого и более высоких порядков", № 4), геометрические места точек М, расстояния которых от двух фиксированных точек 1 и 2, называемых фокусами, умноженные на данные числа, имеют постоянную сумму с, то есть mMF1 + + nMF2 = с. уравнение в прямоугольных координатах:
(x + y" —2rx)2 — l2(x2 + y2) — k = 0,
где r, l и k — некоторые постоянные, связанные с параметрами m, n и d; в полярных координатах:
(n2 — m2)(2 + 2((mc — n2d cos () + n2d2 — с2 = 0.
Помимо фокусов 1 и 2, имеется и третий фокус 3, равноправный с каждым из них. При m = 1, n = 1 овал Декарта превращается в эллипс; при m = 1 и n = —1 — в гиперболу. Частным случаем овала является также улитка Паскаля. Овалы впервые исследовались Р. Декартом (1637).
Овалы Кассини (см. рис. "Алгебраические кривые четвертого и более высоких порядков", № 5), геометрические места точек М, произведение расстояний которых от двух данных точек постоянно. Пусть 1 и 2 точки на оси абсцисс, 12 = 2b, а произведение MF1×MF2 = а2. уравнение в прямоугольных координатах:
(x2 + y2)2 — 2b2 (a2 — y2) = a4 — b4.
Если 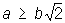 , то овал Кассини — выпуклая кривая; если b < a < , то овал Кассини — выпуклая кривая; если b < a < 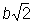 , то кривая имеет вид овала с двумя утолщениями; при а = b овал Кассини превращается в лемнискату, наконец, при b > а овал Кассини является двусвязной кривой. Впервые рассмотрена Дж. Кассини (17 в.). , то кривая имеет вид овала с двумя утолщениями; при а = b овал Кассини превращается в лемнискату, наконец, при b > а овал Кассини является двусвязной кривой. Впервые рассмотрена Дж. Кассини (17 в.).
Улитка Паскаля (см. рис. "Алгебраические кривые четвертого и более высоких порядков", № 6), геометрическое место точек М и M", расположенных на прямых пучка (центр которого О лежит на окружности радиуса R) на расстоянии а по обе стороны от точки Р пересечения прямых с окружностью; т. о., PM = PM" = а. уравнение в прямоугольных координатах: (x2 + y2 — 2Rx)2 — а2(х2 + y2) = 0, в полярных координатах: r = 2R cos j + а. При а = 2R петля стягивается в точку, в этом случае улитка Паскаля превращается в кардиоиду. Название по имени французского ученого Э. Паскаля (1588—1651), впервые изучавшего ее.
Астроида (от греч. ástron — звезда и éidos — вид) (см. рис. "Алгебраические кривые четвертого и более высоких порядков", № 7), кривая, описываемая точкой подвижной окружности, которая касается изнутри неподвижной окружности вчетверо большего радиуса и катится по ней без скольжения. уравнение в прямоугольных координатах: x2/3 + y2/3 = а2/3, где а — радиус неподвижной окружности. Астроида — линия 6-го порядка.
Розы (см. рис. "Алгебраические кривые четвертого и более высоких порядков", № 8), кривые, полярное уравнение которых: r = a sin mj; если m — рациональное число, то розы — алгебраической Л (геометрич. понятие) четного порядка. При m нечетном роза состоит из от лепестков, при m четном — из 2m лепестков; при m рациональном лепестки частично покрывают друг друга.
Синусоидальные спирали, синус-спирали (см. рис. "Алгебраические кривые четвертого и более высоких порядков", № 9), кривые, полярное уравнение которых rm = am cosmj; если m — рациональное число, то эти Л (геометрич. понятие) — алгебраические. Частные случаи: m = 1 — окружность, m = — 1 — прямая, m = 2 — лемниската Бернулли, m = —2 — равнобочная гипербола, m = 1/2 — кардиоида, m = — 1/2 — парабола. При целом m > 0 Л (геометрич. понятие) состоит из m лепестков, каждый из которых лежит внутри угла, равного p/m, при рациональном m > 0 лепестки могут частично покрывать друг друга; если m < 0, то Л (геометрич. понятие) состоит из от бесконечных ветвей.
Большой интересный класс составляют трансцендентные Л (геометрич. понятие) К ним относятся графики тригонометрических функций (синусоида, тангенсоида), логарифмической функции, показательной функции, гиперболических функций, а также следующие Л (геометрич. понятие):
Квадратриса (см. рис. "Трансцендентные кривые", № 1). Пусть прямая MN равномерно вращается против часовой стрелки вокруг точки О, а прямая А"В" равномерно движется справа налево, оставаясь параллельной . Далее, пусть за время движения A" от AB до прямая MN поворачивается на прямой угол и переходит из положения OA = r в положение . Геометрическое место точек Р пересечения прямых MN и A" и есть квадратриса. уравнение в прямоугольных координатах: 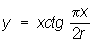 ; в полярных координатах: ; в полярных координатах: 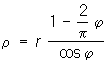 . Часть квадратрисы, заключенная в квадрате OABC, была известна древнегреч. математикам. Открытие квадратрисы приписывается Гиппию Элидскому (5 в. до н. э.), использовавшему ее для решения задачи о трисекции угла. Динострат (4 в. до н. э.) с помощью квадратрнсы выполнил квадратуру круга. . Часть квадратрисы, заключенная в квадрате OABC, была известна древнегреч. математикам. Открытие квадратрисы приписывается Гиппию Элидскому (5 в. до н. э.), использовавшему ее для решения задачи о трисекции угла. Динострат (4 в. до н. э.) с помощью квадратрнсы выполнил квадратуру круга.
Трактриса (см. рис. "Трансцендентные кривые", № 2), кривая, для которой длина отрезка касательной от точки касания М до точки Р пересечения с данной прямой есть величина постоянная, равная а. Уравнение в прямоугольных координатах:
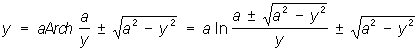 . .
Цепная линия (см. рис. "Трансцендентные кривые", № 3), кривая, форму которой принимает гибкая однородная и нерастяжимая тяжелая нить, концы которой закреплены в двух точках. уравнение в прямоугольных координатах: у = a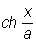 = а (ex/a + е-х/a)/2. = а (ex/a + е-х/a)/2.
Циклоида (от греч. kykloeides — кругообразный) (см. рис. "Трансцендентные кривые", № 4), кривая, которую описывает точка Р, расположенная на расстоянии а от центра круга радиуса r, катящегося без скольжения по прямой линии. Если Р лежит на окружности круга (r = а), получают обыкновенную циклоиду (см. рис. "Трансцендентные кривые", № 4а), если она лежит внутри круга (r > а), — укороченную циклоиду (см. рис. "Трансцендентные кривые", № 4б), если точка вне круга (r < а), — удлиненную циклоиду (см. рис. "Трансцендентные кривые", № 4в). Две последние Л (геометрич. понятие) называют трохоидами. Уравнение в параметрической форме:
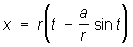 , , 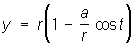 . .
Среди трансцендентных Л (геометрич. понятие) особый класс составляют спирали (от греч. spéira, буквально — витое), плоские кривые линии, бесчисленное множество раз обходящие некоторую точку, с каждым обходом приближаясь к ней или с каждым обходом удаляясь от нее. Если выбрать эту точку за полюс системы координат, то полярное уравнение спирали r = f(j) таково, что f(j + 2p) > f(j) или f(j + 2p) < f(j) при всех j. Из спиралей наиболее известны:
Архимедова спираль (см. рис. "Трансцендентные кривые", № 5), кривая, описываемая точкой, равномерно движущейся по прямой в то время, как эта прямая равномерно вращается в плоскости вокруг точки О. уравнение в полярных координатах: r = aj, где а — постоянная. Эта спираль изучалась Архимедом (3 в. до н. э.) в связи с задачами трисекции угла и квадратуры круга.
Гиперболическая спираль (см. рис. "Трансцендентные кривые", № 6), кривая, описываемая точкой М, движущейся по вращающейся прямой OA, так, что ее расстояние от центра вращения меняется обратно пропорционально углу поворота. Уравнение в полярных координатах: r = а/j.
Жезл (см. рис. "Трансцендентные кривые", № 7), кривая, уравнение которой в полярных координатах: 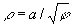 . Каждому значению j соответствуют два значения r — положительное и отрицательное. Кривая состоит из двух ветвей, каждая из которых асимптотически приближается к полюсу. . Каждому значению j соответствуют два значения r — положительное и отрицательное. Кривая состоит из двух ветвей, каждая из которых асимптотически приближается к полюсу.
Логарифмическая спираль (см. рис. "Трансцендентные кривые", № 8), кривая, уравнение которой в полярных координатах: r = аекj. Была известна многим математикам 17 в.
Спираль Корню (см. рис. "Трансцендентные кривые", № 9), клотоида, кривая, состоящая из двух ветвей, симметричных относительно начала координат. уравнение в параметрической форме:
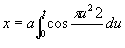 , y = a , y = a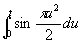 . .
Использовалась французским физиком М. А. Корню (1874) для графич. решения некоторых задач дифракции света.
-ci-спираль (см. рис. "Трансцендентные кривые", № 10), кривая, параметрическое уравнение которой имеет вид
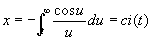 , ,
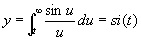 , ,
si(t) и ci(t) — интегральный синус и интегральный косинус.
К циклоиде по способу построения примыкает класс циклоидальных кривых, которые могут быть как алгебраическими, так и трансцендентными. Среди них:
Гипоциклоида (см. рис. "Циклоидальные кривые", № 1а, 1б), кривая, описываемая точкой окружности, катящейся без скольжения по другой окружности внутри ее. Уравнение в параметрической форме:
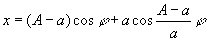 , ,
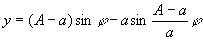 , ,
где А — радиус неподвижной, а а — подвижной окружности. Вид кривой зависит от отношения А/а.
Эпициклоида (см. рис. "Циклоидальные кривые", № 2а, 2б), кривая, описываемая точкой окружности, катящейся без скольжения по другой окружности вне ее. Уравнение получится из уравнения гипоциклоиды заменой а на — а.
Удлиненная гипоциклоида (эпициклоида), кривая, описываемая точкой, лежащей вне окружности, которая катится без скольжения по другой окружности внутри (вне) ее (см. рис. "Циклоидальные кривые", № 3а, 4д). Аналогично определяется укороченная гипоциклоида (эпициклоида) (см. рис. "Циклоидальные кривые", № 3б, 4б). Удлиненные и укороченные гипоциклоиды и эпициклоиды иногда называются гипо- и эпитрохоидами.
В. И. Битюцков, Ю. А. Горьков, А. Б. Иванов.
Лит.: Маркушевич А. И., Замечательные кривые, 2 изд., М. — Л (геометрич. понятие), 1952; Савелов А. А., Плоские кривые. Систематика, свойства, применения (Справочное руководство), М., 1960; Пархоменко А. С., Что такое линия, М., 1954; Погорелов А. В., Дифференциальная геометрия, 5 изд., М., 1969; Уокер А., Алгебраические кривые, пер. с англ., М., 1952; Loria G., Spezielle algebraische und transzendente ebene Kurven. Theorie und Geschichte, 2 Aufl., Bd 1—2, Lpz. — ., 1910—11.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 11:50:03
|

|

|
 |
|

|
 |
 |
 |
|