
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Линейные дифференциальные уравнения | Линейные дифференциальные уравнения (далее Л), дифференциальные уравнения вида
y(n) + p1(x) у(n-1) + ... + pn(x)y = f(x), (1)
где у = y(x) — искомая функция, y(n), у(n-1),..., y" — ее производные, a p1(x), p2(x),..., pn(x) (коэффициенты) и f(x) (свободный член) — заданные функции (см. Дифференциальные уравнения). В уравнение (1) искомая функция у и ее производные входят в 1-й степени, т. е. линейно, поэтому оно называется линейным. Если f(x) º 0, то уравнение (1) называется однородным, в противном случае — неоднородным. Общее решение y0 = y0(x) однородного Л при условии непрерывности его коэффициентов pk(x) выражается формулой:
y0 = 1y1(x) + С2у2(х) + ... + nyn(x),
где 1, 2,..., n — произвольные постоянные и y1(x), у2(х),..., yn(x) — линейно независимые (см. Линейная зависимость) частные решения, образующие т. н. фундаментальную систему решений. Критерием линейной независимости решений служит неравенство нулю (хотя бы в одной точке) определителя Вроньского (вронскиана):
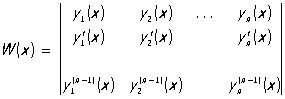 (2) (2)
Общее решение у = у(х) неоднородного Л (1) имеет вид:
y = y0+,
где y0 = y0(x) — общее решение соответствующего однородного Л и = (x) — частное решение данного неоднородного Л Функция (x) может быть найдена по формуле:
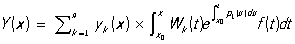 , ,
где yk(x) — решения, составляющие фундаментальную систему решений однородного Л, и k(x) — алгебраическое дополнение элемента yk(n-1)(x) в определителе (2) Вроньского (x).
Если коэффициенты уравнения (1) постоянны: pk(x) = ak (k = 1, 2, ..., n), то общее решение однородного уравнения выражается формулой:
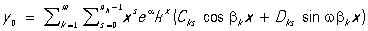 , ,
где ak ± ibk (k = 1, 2, ..., m; 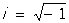 ) — корни т. н. характеристического уравнения: ) — корни т. н. характеристического уравнения:
ln + a1ln-1 + ... +an = 0,
nk — кратности этих корней и ks, Dks — произвольные постоянные.
Пример. Для Л y"` + у = 0 характеристическое уравнение имеет вид: l3 + 1 = 0. Его корнями являются числа:
l1 = -1; l2 = 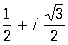 и l3 = и l3 = 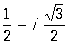
Следовательно, общее решение этого уравнения таково:
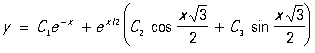 . .
Системы Л имеют вид:
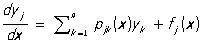 (3) (3)
(j = 1, 2, ..., n).
Общее решение однородной системы Л (получаемой из системы (3), если все fj(x) º 0) дается формулами:
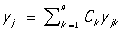
(j = 1, 2, ..., n)
где yj1, yj2, ..., yjn — линейно независимые частные решения однородной системы (т. е. такие, что определитель ½yjk(x)½ ¹ 0 хотя бы в одной точке).
В случае постоянных коэффициентов pjk(x) = ajk частные решения однородной системы следует искать в виде:
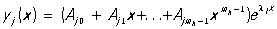
(j = 1, 2, ..., n),
где Ajs — неопределенные коэффициенты, a lk — корни характеристического уравнения
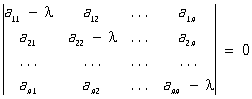
и mk — кратность этих корней. Полный анализ всех возможных здесь случаев проводится с помощью теории элементарных делителей (см. Нормальная (жорданова) форма матриц).
Для решения Л и систем Л с постоянными коэффициентами применяются также методы операционного исчисления.
Лит.: Степанов В. В., Курс дифференциальных уравнений, 8 изд., М., 1959; Смирнов В. И., Курс высшей математики, т. 2, 20 изд., М., 1967; т. 3, ч. 2, 8 изд., М., 1969; Понтрягин Л. С., Обыкновенные дифференциальные уравнения, 3 изд., М., 1970. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 11:58:43
|

|

|
 |
|

|
 |
 |
 |
|