|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Лагранжа уравнения | Лагранжа уравнения (далее Л),
1) в гидромеханике — уравнения движения жид кой среды, записанные в переменных Лагранжа, которыми являются координаты частиц среды. Из Л определяется закон движения частиц среды в виде зависимостей координат от времени, а по ним находятся траектории, скорости и ускорения частиц. Обычно этот путь исследования оказывается достаточно сложным, и при решении большинства гидромеханических задач идут другим путем, используя Эйлера уравнения гидромеханики. Л применяют главным образом при изучении колебательных движений жидкости.
Л являются уравнениями в частных производных и имеют вид:
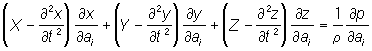
(i = 1, 2, 3),
где t — время, х, у, z — координаты частицы, a1, a2, a3 — параметры, которыми отличаются частицы друг от друга (например, начальные координаты частиц), X, , Z — проекции объемных сил, р — давление, r — плотность.
Решение конкретных задач сводится к тому, чтобы, зная X, , Z, а также начальные и граничные условия, найти х, у, z, р, r как функции t и а1, a2, a3. При этом надо использовать еще неразрывности уравнение (тоже в переменных Лагранжа) и уравнение состояния в виде r = f(Р) (для несжимаемой жидкости r — const).
2) В общей механике — уравнения, применяемые для изучения движения механической системы, в которых за величины, определяющие положение системы, выбирают независимые между собой параметры, называют обобщенными координатами. Впервые получены Ж. Лагранжем в 1760.
Движение механической системы можно изучать, используя или непосредственно уравнения, которые дает 2-й закон динамики, или получаемые как следствия из законов динамики общие теоремы (см. Динамика). Первый путь приводит к необходимости решать большое число уравнений, зависящее от числа точек и тел, входящих в систему; кроме того, эти уравнения содержат дополнительные неизвестные в виде реакций наложенных связей (см. Связи механические). Все это приводит к большим математическим трудностям. Второй путь требует применения каждый раз разных теорем и для сложных систем приводит в итоге к тем же трудностям.
Л дают для широкого класса механических систем единый и достаточно простой метод составления уравнений движения, не зависящий от вида (сложности) конкретной системы. Большое преимущество Л состоит в том, что число их равно числу степеней свободы системы и не зависит от количества входящих в систему точек и тел. Например, машины и механизмы состоят из многих тел (деталей), а имеют обычно 1—2 степени свободы; следовательно, изучение их движения потребует составления лишь 1—2 Л Кроме того, при идеальных связях из Л автоматически исключаются все неизвестные реакции связей. По этим причинам Л широко используются при решении многих задач механики, в частности в динамике машин и механизмов, в теории колебаний, теории гироскопа и др. Кроме этого, в случае, когда на систему действуют только потенциальные силы, Л приводятся к виду, позволяющему использовать их (при соответствующем обобщении понятий) не только в механике, но и в др. областях физики.
Для голономных систем Л в общем случае имеют вид:
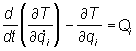
(i = 1,2, ..., n),
где qi — обобщенные координаты, число которых равно числу n степеней свободы системы, 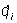 — обобщенные скорости, Qi — обобщенные силы, Т — кинетическая энергия системы, выраженная через qi и  .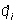
Для составления уравнений (1) надо найти выражение Т и вычислить по заданным силам Qi. После подстановки Т в левые части уравнения (1) будут содержать координаты qi и их первые и вторые производные по времени, т. е. будут дифференциальными уравнениями 2-го порядка относительно qi. Интегрируя эти уравнения и определяя постоянные интегрирования по начальным условиям, находят зависимости qi(t), т. е. закон движения системы в обобщенных координатах.
Когда на систему действуют только потенциальные силы, Л принимают вид:
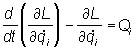
(i = 1,2, ..., n),
где L = Т — П — т. н. функция Лагранжа, а П — потенциальная энергия системы. Эти уравнения используются и в др. областях физики.
Уравнения (1) и (2) называют еще Л 2-го рода. Кроме них, есть Л 1-го рода, имеющие вид обычных уравнений в декартовых координатах, но содержащие вместо реакций связей пропорциональные им неопределенные множители. Особыми преимуществами эти уравнения не обладают и используются редко, главным образом для отыскания реакций связей, когда закон движения системы найден другим путем, например с помощью уравнений (1) или (2).
Лит. см. при ст. Механика. О Л в гидромеханике см. Кочин Н. Е., Кибель И. А., Розе Н. В., Теоретическая гидромеханика, 6 изд., ч. 1, М., 1963.
С. М. Тарг. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 21.11.2024 12:19:10
|
|
|
|
|
|
|
|
|
|
|
