
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Комплексные числа | Комплексные числа (далее К) числа вида х + iy, где х и у — действительные числа, а i — так называемая мнимая единица (число, квадрат которого равен —1); х называют действительной частью, а у — мнимой частью К z = х +iy (обозначают х =z, у=Imz). Действительные числа — частный случай К (при у = 0); К, не являющиеся действительными (у ¹ 0), называют мнимыми числами; при х = 0 К Называют чисто мнимым. К z = х+iy и z = х—iy называют комплексно-сопряженными. Арифметические действия над К производятся по обычным правилам действий над многочленами с учетом условия i2=—1. Геометрически каждое К х + iy изображается точкой плоскости, имеющей прямоугольные координаты х и у (см. рис.). Если полярные координаты этой точки обозначить через r и j:, то соответствующее К можно представить в виде:
r (cos j + i sin j)
(тригонометрическая, или полярная, форма К);
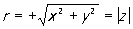 называют модулем К х+iy, а j = arg z — аргументом его. Тригонометрическая форма К особенно удобна для действий возведения в степень и извлечения корня: называют модулем К х+iy, а j = arg z — аргументом его. Тригонометрическая форма К особенно удобна для действий возведения в степень и извлечения корня:
(r (cos j + i sin j)) n = rn (cos nj + i sin nj),
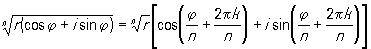 , в частности , в частности
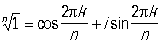 , k = 0, 1, …, n—1 , k = 0, 1, …, n—1
По своим алгебраическим свойствам совокупность К образует поле. Это поле алгебраически замкнуто, т. е. любое уравнение xn + a1xn-1+...+an =0; где a1,..., an — К, имеет (при учете кратности) среди К точно n корней.
Уже в древности математики сталкивались в процессе решения некоторых задач с извлечением квадратного корня из отрицательных чисел; в этом случае задача считалась неразрешимой. Когда же в 1-й половине 16 в. были найдены формулы для решения кубических уравнений, оказалось, что в так называемом неприводимом случае действительные корни уравнений с действительными коэффициентами получаются в результате действий над К Это содействовало признанию К Первое обоснование простейших действий с К встречается у Р. Бомбелли в 1572. Однако долгое время к К относились, как к чему-то сверхъестественному. Так, Г. Лейбниц в 1702 писал: "Мнимые числа — это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием". В 1748 Л. Эйлер нашел замечательную формулу eij = cosj + isinj, явившуюся первым важным результатом теории функций комплексного переменного, но истинный характер К выяснился лишь к концу 18 в., когда была открыта их геометрическая интерпретация (см. выше). Термин "К" предложен К. Гауссом в 1831. Введение К делает многие математические рассмотрения более единообразными и ясными и является важным этапом в развитии понятия о числе (см. Число). К Употребляются теперь при математическом описании многих вопросов физики и техники (в гидродинамике, аэромеханике, электротехнике, физике и т.д.). Основные разделы классического математического анализа приобретают полную ясность и законченность только при использовании К, чем обусловливается центральное место, занимаемое теорией функций комплексного переменного. См. Аналитические функции.
Лит.: Маркушевич А. И., К и конформные отображения, 2 изд., М., 1960; Курош А. Г., Курс высшей алгебры, 9 изд., М., 1968.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 11:52:20
|

|

|
 |
|

|
 |
 |
 |
|