
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Колебания кристаллической решетки | Колебания решетки (далее К) один из основных видов внутренних движений твердого тела, при котором составляющие его частицы ( или ионы) колеблются около положений равновесия — узлов решетки. К, например, в виде стоячих или бегущих звуковых волн возникают всякий раз, когда на действует внешняя сила, изменяющаяся со временем. Однако и в отсутствие внешних воздействий в находящемся в тепловом равновесии с окружающей средой, устанавливается стационарное состояние колебаний, подобно тому как в газе устанавливается стационарное распределение или молекул по скорости их поступательного движения.
Характер этих колебаний зависит от симметрии числа в его элементарной ячейке, типа химической связи, а также от вида и концентрации дефектов в кристаллах. Смещения и в процессе колебаний тем больше, чем выше температура, но они гораздо меньше постоянной решетки вплоть до температуры плавления, когда твердое тело превращается в жидкость. Силы, которые стремятся удержать в положениях равновесия, пропорциональны их относительным смещениям так, как если бы они были связаны друг с другом пружинками (рис. 1). Представление в виде совокупности частиц, связанных идеально упругими силами, называется гармоническим приближением.
В состоящем из элементарных ячеек по n в каждой, существует 3nN — 6 типов простейших колебаний в виде стоячих волн, называемых нормальными (либо собственными) колебаниями, или модами. Их число равно числу степеней свободы у совокупности частиц за вычетом трех степеней свободы, отвечающих поступательному, и трех — вращательному движению как целого (см. Степеней свободы число). Числом 6 можно пренебречь, так как 3nN — величина ~ 1022—1023 для 1 см3
В процессе нормального колебания все частицы колеблются около своих положений равновесия с одной и той же постоянной частотой w по закону u ~ sinw·t подобно простому гармоническому осциллятору. В одновременно могут присутствовать все возможные нормальные колебания, причем каждое протекает так, как если бы остальных не было вовсе. Любое движение в не нарушающее его микроструктуры, может быть представлено в виде суперпозиции нормальных колебаний
Каждую стоячую волну нормального колебания можно, в свою очередь, представить в виде двух упругих плоских бегущих волн, распространяющихся в противоположных направлениях (нормальные волны). Плоская бегущая волна, помимо частоты w, характеризуется волновым вектором k, определяющим направление движения фронта волны и длину волны l= 2 p/k, а также поляризацией, которая определяет характер индивидуального движения частиц. В общем случае имеет место эллиптическая поляризация, когда каждый описывает эллипс около своего положения равновесия (рис. 2), при этом нормаль к плоскости эллипса не совпадает по направлению с k. Эллиптические орбиты одинаковы для идентичных занимающих эквивалентные положения в решетке. В тех где каждый узел является центром симметрии (см. Симметрия кристаллов), все нормальные волны плоскополяризованы: в любом нормальном колебании совершают возвратно-поступательные движения около своих положений равновесия.
Дисперсия нормальных волн. При каждом значении k существует 3n типов нормальных волн с различной поляризацией. Они нумеруются целочисленной переменной s = 1, 2... 3n и называется ветвями нормальных колебаний. Для волн данного типа s величины w и k не могут быть произвольными, а связаны между собой определенным соотношением w = w(k, s), называется законом дисперсии. Например, если представить в виде совокупности одинаковых массы т, расположенных на равных расстояниях а друг от друга и связанных попарно пружинами с жесткостью g так, что они образуют бесконечную цепочку и могут смещаться только вдоль ее оси (рис. 3, а), то элементарная ячейка состоит из одной частицы и существует одна ветвь частоты нормальных колебаний с законом дисперсии:
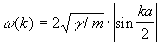 . .
У двухатомной линейной цепочки (рис. 3, б) ячейка содержит 2 частицы с массами т и М и имеется 2 ветви с более сложным законом дисперсии (рис. 4): 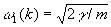 , , 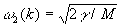 , , 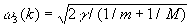 , (M > m). , (M > m).
Упругие волны в всегда обладают дисперсией. В частности, их фазовая скорость, как правило, отличается от групповой, с которой по переносится энергия колебаний. В то время как частота w упругих волн, распространяющихся в непрерывной среде, неограниченно возрастает с ростом k, в благодаря периодическому расположению и конечной величине связывающих их сил существует некоторая максимальная частота колебаний wмакс (обычно ~1013 гц). Собственные частоты могут не сплошь заполнять интервал от w = 0 до w = wмакс, в нем могут быть пустые участки (запрещенные зоны), разделяющие две следующие друг за другом ветви. Запрещенной зоны между соседними ветвями нет, если ветви перекрываются. Колебания, соответствующие запрещенным зонам и с частотой w > wмакс, не могут распространяться в они быстро затухают.
Акустическая и оптическая ветви. Три первые ветви колебаний с s = 1,2,3 называются акустическими. В случае, когда длина волны l значительно превышает наибольший из периодов пространственной решетки (k — мало), они характеризуются линейным законом дисперсии w = c ·k. Это обычные звуковые волны, а с — фазовая скорость их распространения, зависящая от направления распространения и поляризации. Они плоскополяризованы в одном из трех взаимно перпендикулярных направлений соответственно трем значениям s = 1, 2, 3 и соответствуют колебаниям как сплошной среды. В анизотропном ни одно из этих направлений обычно не совпадает с направлением распространения волны, т. е. с k. Лишь в упругой изотропной среде звуковые волны имеют чисто продольную и чисто поперечную поляризации. Акустические ветви охватывают диапазон частот от нуля до ~ 1013 гц. Однако с уменьшением длины волны закон дисперсии становится более сложным.
Для остальных 3·(n—1) ветвей частоты смещения в процессе колебаний, соответствующих большой длине волны, происходят так, что центр масс отдельной элементарной ячейки покоится. В ионных кристаллах, элементарная ячейка которых состоит из ионов противоположных знаков, движение такого типа можно возбудить переменным электрическим полем, например световой волной, с частотой, лежащей, как правило, в инфракрасной области. Поэтому эти ветви называются оптическими. Свое название акустическая ветвь получила по начальному участку (), начальный участок акустической ветви — обычный звук.
Фононы. Каждой бегущей плоской волне с вектором k и частотой w можно поставить в соответствие совокупность движущихся квазичастиц с импульсом р = 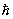 k и энергией E = k и энергией E = 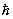 w, где w, где 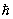 — Планка постоянная (см. Корпускулярно-волновой дуализм). Эти квазичастицы являются квантами поля К и называются фононами по аналогии с фотонами — квантами электромагнитного поля. — Планка постоянная (см. Корпускулярно-волновой дуализм). Эти квазичастицы являются квантами поля К и называются фононами по аналогии с фотонами — квантами электромагнитного поля.
Влияние К на свойства осциллируют около положений равновесия тем интенсивнее, чем выше температура Когда амплитуда колебаний превышает некоторое критическое значение, наступает плавление и структура разрушается. С понижением температуры амплитуда уменьшается и становится минимальной при Т = 0 К. Полная остановка с обращением их энергии в нуль, в силу законов квантовой механики, невозможна, и они при Т = 0 К совершают "нулевые" колебания. Так как энергия "нулевых" колебаний обычно недостаточна, чтобы твердое тело расплавилось, то с понижением температуры все жидкости рано или поздно затвердевают. Единственным исключением является который остается жидким вплоть до температуры 0 К и затвердевает лишь под давлением.
Количественной характеристикой способности запасать тепло в виде энергии колебаний служит решеточная теплоемкость. Будучи отнесенной к одному она оказывается приближенно равной 3kБ (kБ — Больцмана постоянная) при высоких температурах (Дюлонга и Пти закон) и пропорциональной Т3, когда Т приближается к 0 К.
В металлах и полупроводниках, помимо или ионов, имеются также свободные электроны, которые в присутствии электрического поля создают электрический ток. Законы их движения таковы, что они беспрепятственно проходят сквозь идеальный кристалл из ионов, находящихся в состоянии "нулевых" колебаний. Поэтому сопротивление электрическому току при Т =0 К возникает лишь постольку, поскольку в всегда имеются дефекты, рассеивающие электроны. Однако при температурах Т > 0 К колебания хаотически нарушают идеальную периодичность решетки и создают дополнительное — решеточное, или фононное, электросопротивление. Сталкиваясь с осциллирующими электроны передают остову часть энергии своего направленного поступательного движения, которая выделяется в виде джоулева тепла.
Ангармонизм. В действительности возвращающие силы не строго пропорциональны смещениям из положений равновесия и колебания не являются строго гармоническими (ангармонизм). Нелинейность междуатомных сил мала, поскольку малы амплитуды колебаний. Однако
благодаря ей отдельные нормальные колебания не являются независимыми, а оказываются связанными друг с другом и между ними возможен резонанс, как в системе связанных маятников.
В процессе установления термодинамического равновесия в ангармонизм играет ту же роль, что и столкновение частиц в газе. Он, в частности, объясняет тепловое расширение отклонение от Дюлонга и Пти закона в области высоких температур, а также отличие друг от друга изотермических и адиабатических упругих постоянных твердого тела и их зависимость от температуры и давления (см. Упругость).
При неравномерном нагревании твердого тела в нем возникают потоки тепла. В металлах большая часть его переносится электронами, а в диэлектриках — нормальными волнами (фононами). Поэтому если иметь в виду диэлектрики или решеточную часть теплопроводности металлов, то в отсутствии ангармонизма тепловой поток распространялся бы со скоростью нормальных волн, то есть приблизительно со скоростью звука. Благодаря ангармонизму волны в тепловом потоке обмениваются энергией и интерферируют друг с другом. В процессе такой интерференции происходит потеря суммарного импульса теплового потока. В результате возникает теплосопротивление, а тепловая энергия переносится с диффузионной скоростью, гораздо меньшей скорости распространения упругой энергии, например звуковой волны. Ангармонизм является также одной из причин затухания ультразвука в
Локальные и квазилокальные колебания. На характер К существенно влияют дефекты решетки. Жесткость межатомных связей и массы частиц в области дефекта отличаются от таковых для идеального называются эталонным или матрицей. В результате этого нормальные волны не являются плоскими. Например, если дефект — это примесный массы т0, связанный с соседями пружинами жесткости g0, то может случиться, что его собственная частота колебаний 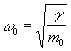 попадет в запрещенную область частот матрицы. В таком колебании активно участвует лишь примесный поэтому оно и называется локальным. Так как в реальном дефектов всегда много (см. Дефекты в кристаллах), то локальное колебание, будучи возбужденным на одном дефекте, может перейти на другой, как при резонансе одинаковых слабо связанных маятников. Поэтому локальные колебания обладают целым спектром частот, которые образуют примесную зону частот К попадет в запрещенную область частот матрицы. В таком колебании активно участвует лишь примесный поэтому оно и называется локальным. Так как в реальном дефектов всегда много (см. Дефекты в кристаллах), то локальное колебание, будучи возбужденным на одном дефекте, может перейти на другой, как при резонансе одинаковых слабо связанных маятников. Поэтому локальные колебания обладают целым спектром частот, которые образуют примесную зону частот К
Наряду с локальными колебаниями в области низких частот могут существовать так называемые квазилокальные колебания. В частности, такие колебания есть в с тяжелыми примесными Квазилокальные колебания при низких температурах резко увеличивают решеточную теплоемкость, коэффициент термического расширения, тепло- и электросопротивления. Так, например, 2—3% примесных в 10 раз более тяжелых, чем матрицы, способны при малых Т удвоить решеточную теплоемкость и коэффициент термического расширения.
Локальные колебания протяженных дефектов, например дислокации, распространяются вдоль них в виде волн, но в матрицу, как и в случае точечных дефектов, не проникают. Частоты этих колебаний могут принадлежать как запрещенной, так и разрешенной области частот матрицы, отличаясь от них законом дисперсии. Таковы, например, звуковые поверхностные волны, возникающие у плоской границы твердого тела (волны Рэлея).
Экспериментальные методы изучения К разнообразны. Одним из методов изучения локальных и квазилокальных К служит их возбуждение при помощи инфракрасного излучения. Оно сопровождается резонансным уменьшением прозрачности и позволяет не только обнаружить эти колебания, но и определить их частоты.
Исследования неупругого рассеяния нейтронов в позволяют определить закон дисперсии и поляризацию нормальных колебаний. Закон дисперсии может быть также восстановлен с помощью диффузного рассеяния рентгеновских лучей. Мессбауэра эффект позволяет непосредственно определить среднеквадратичные смещения и импульсы в процессе К
Лит.: Займан Дж., Электроны и фононы, пер. с англ., М., 1962; его же, Принципы теории твердого тела, пер. с англ., М., 1966; Лейбфрид Г., Микроскопическая теория механических и тепловых свойств пер. с англ., М., 1963; Марадудин А., Дефекты и колебательный спектр пер. с англ., М., 1968; Ландау Л. Д., Лифшиц Е. М., Статистическая физика, 2 изд., М., 1964: их же, Теория упругости, 3 изд., М., 1965 (Теоретическая физика, т. 7): Киттель Ч., Введение в физику твердого тела, пер. с англ., М., 1963.
Я. А. Иосилевский.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 13:22:38
|

|

|
 |
|

|
 |
 |
 |
|