
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Клинописные математические тексты | Клинописные математические тексты (далее К) математические тексты Древней Вавилонии и Ассирии; охватывают период с начала 2-го тыс. до н. э. и до начала н. э. (см. Вавилоно-ассирийская культура). К написаны клинописью на глиняных пластинках. Среди К имеются математические таблицы (таблицы умножения, таблицы обратных величин, служащие для замены деления умножением, таблицы квадратов и кубов и др.) и специальные математические тексты, содержащие задачи с решениями. Большинство специальных текстов (их известно более сотни) относится ко 2-му тыс. до н. э. Найдены 5—6 текстов 1-го тыс. до н. э., относящихся к эллинистической эпохе, и один текст ассирийской эпохи. В истории математики К имеют большое значение: в них впервые встречаются позиционная система счисления и квадратные уравнения. Вавилонские математики пользовались шестидесятеричной системой счисления, в которой единицы обозначались 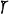 , а десятки , а десятки 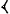 ; эти знаки употреблялись также для обозначения единиц и десятков следующих разрядов; например, число ; эти знаки употреблялись также для обозначения единиц и десятков следующих разрядов; например, число
153 = 2×60 + 33
изображалось так:
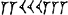
Особенностью вавилонской системы письменного счисления было то, что абсолютная величина чисел оставалась неопределенной. Так, вышеупомянутое число можно было прочесть как 2·602+33·60 = 9180 и как 2+ 33·60-1=233/60; кроме того, в текстах классической эпохи (2-е тыс. до н. э.) отсутствовал знак, соответствующий нашему нулю. Если учесть, что в К отсутствуют записи промежуточных вычислений, то указанное явление проще всего объяснить тем, что промежуточные вычисления производились на счетной доске (типа наших счетов или абака). Тем же самым можно объяснить отсутствие нуля, который при вычислениях на абаке не нужен (столбец, соответствующий отсутствующему разряду, оставлялся пустым). Можно предполагать, что и появление позиционного принципа связано с употреблением счетной доски.
Квадратные уравнения появились у вавилонян в связи с землемерной практикой; эта связь отразилась на терминологии: неизвестные назывались "длина" и "ширина". В дальнейшем неизвестные понимались более абстрактно, так что у вавилонян можно отметить начатки алгебраического мышления.
Лит.: Выгодский М. Я., Арифметика и алгебра в древнем мире, 2 изд., М., 1967; Нейгебауер О., Лекции по истории античных математических наук, пер. с нем., т. 1, М.—Л., 1937; Mathematische Keilschrift-Texte, hrsg. von О. Neugebauer, 1, ., 1935; Mathematical cuneiform texts, ed. by О. Neugebauer and A. Sachs, New Haven, 1945.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 12:08:44
|

|

|
 |
|

|
 |
 |
 |
|