
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Аномалии | Аномалии (далее А) истинная, средняя, эксцентрическая (в небесной механике), величины, определяющие положение небесного тела (планеты, спутника и т. п.) на эллиптической орбите. Истинная А — угол между направлением на перицентр П (перигей, перигелий) орбиты и радиусом-вектором небесного тела (см. рис.); отсчитывается от радиуса-вектора ОП в направлении движения тела. В соответствии со вторым Кеплера законом истинная А изменяется со временем неравномерно: быстрее, когда небесное тело движется вблизи перицентра П, и медленнее — вблизи апоцентра А. Зависимость истинной аномалии от времени выражается с помощью равномерно изменяющейся средней аномалии М. Средняя А — угол М между направлением на перицентр и радиусом-вектором некоторой фиктивной точки, движущейся по орбите с постоянной угловой скоростью, равной средней угловой скорости реального небесного тела, и проходящей одновременно с ним через перицентр и апоцентр. При движении тела от П до А небесное тело опережает фиктивную точку ( > M), а затем, при движении от А до П, отстает от нее ( < M). Средняя аномалия M0 в некоторый ("начальный") момент времени t0 принимается за один из элементов орбиты. Эксцентрическая А — угол Е с вершиной в центре С орбиты (в отличие от истинной и средней А, имеющих вершину в центре масс центрального тела) между направлениями на перицентр и на фиктивную точку Р, смысл которой ясен из рисунка (ПРА — окружность с центром в центре орбиты и радиусом, равным большой полуоси орбиты; PSQ — перпендикуляр к большой оси орбиты ПА, проведенный через небесное тело ).
Эксцентрическая А является вспомогательной величиной для перехода от средней А к истинной А при решении задачи, связанной с определением положения небесного тела на орбите в заданный момент t. Средняя А, определяемая уравнением:
М = M0 + n(t - t0),
где n — среднее движение небесного тела по орбите, позволяет вычислить эксцентрическую А с помощью Кеплера уравнения:
Е - е sin Е = М,
где е — эксцентриситет орбиты. После этого истинная А находится решением уравнения:
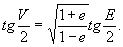
Аналогично решается обратная задача: определение момента прохождения небесным телом заданной точки орбиты. Для решения указанных задач составлены таблицы, позволяющие находить истинную А непосредственно по заданным значениям средней А, а также по значениям истинной А определять среднюю А
Лит.: Жонголович И. Д., Амелин В. М., Сборник таблиц и номограмм для обработки наблюдений искусственных спутников Земли, М.—Л., 1960; Дубошин Г. Н., Небесная механика, М., 1963.
Н. П. Ерпылев.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 13:20:01
|

|

|
 |
|

|
 |
 |
 |
|