
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Квадратичный вычет | Квадратичный вычет (далее К) понятие теории чисел. К по модулю m — число а, для которого сравнение x2 º а (mod m) имеет решение: при некотором целом х число x2—a делится на m; если это сравнение не имеет решений, то а называют квадратичным невычетом. Например, если m = 11, то число 3 будет К, так как сравнение x2 º 3 (mod 11) имеет решения х = 5, х = 6, а число 2 будет невычетом, т.к. не существует чисел х, удовлетворяющих сравнению x2 º 2 (mod 11). К являются частным случаем вычетов степени n для n = 2. Если m равно простому нечетному числу р, то среди чисел 1, 2,..., р—1 имеется (р—1)/2 К и (р—1)/2 квадратичных невычетов. Для изучения К по простому модулю р вводится Лежандра символ 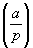 , определяемый так: если а взаимно просто с р, то полагают , определяемый так: если а взаимно просто с р, то полагают 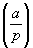 = 1, когда а — К, и = 1, когда а — К, и 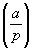 = — 1, когда а — квадратичный невычет. Основной теоремой в этом круге вопросов является так называемый закон взаимности К: если р и q — простые нечетные числа, то = — 1, когда а — квадратичный невычет. Основной теоремой в этом круге вопросов является так называемый закон взаимности К: если р и q — простые нечетные числа, то
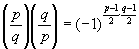 . .
Эту закономерность открыл около 1772 Л. Эйлер, современная формулировка дана А. Лежандром, полное доказательство впервые дал в 1801 К. Гаусс. Удобным обобщением символа Лежандра является Якоби символ. Закон взаимности К получил многочисленные обобщения в теории алгебраических чисел. И. М. Виноградовыми др. учеными изучалось распределение К и суммы значений символа Лежандра.
Лит.: Виноградов И. М., Основы теории чисел, 8 изд., М., 1972. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 21.11.2024 14:20:12
|

|

|
 |
|

|
 |
 |
 |
|